Nanostruktury magnetyczne na podłożach ze złamaną symetrią translacyjną
Wstęp
Naruszenie symetrii translacyjnej powierzchni podłoża, prowadzi do modyfikacji struktury elektronowej, co w efekcie istotnie zmienia właściwości magnetyczne. Jest to szczególnie widoczne w układach niskowymiarowych, gdzie wpływ powierzchni, a zwłaszcza niemagnetycznego podłoża, odgrywa często decydującą rolę. Jednym z rodzajów obiektów o obniżonej wymiarowości są ultracienkie warstwy magnetyczne. W fizyce materii skondensowanej pojęcie ultracienkiej warstwy oznacza warstwę o grubości kilku odległości międzyatomowych [9]. Warstwy te posiadają wiele interesujących własności [10], które istotnie różnią się od odpowiednich własności cienkich warstw o rozmiarach mikronowych, czy też materiałów litych.
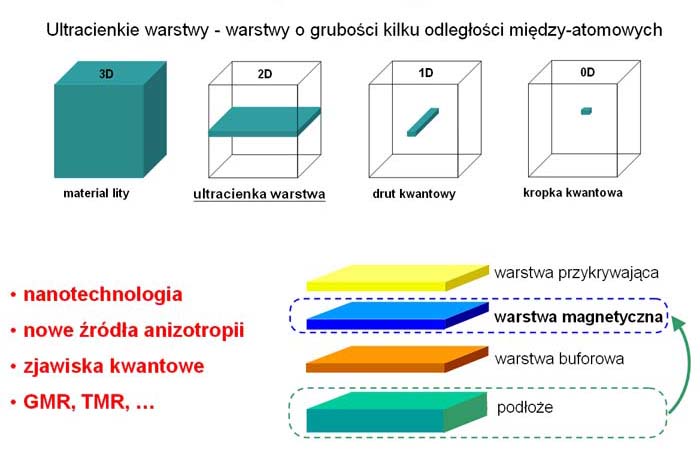
Rys. 1 Ultracienkie struktury magnetyczne
Wiele interesujących zjawisk fizycznych w świecie rozwoju nanotechnologii obiektów magnetycznych odkryto w ciągu ostatnich kilkunastu lat. We współczesnej fizyce, ogromne znaczenie poznawcze takich obiektów jest związane z odkryciami wielu ciekawych efektów, jak chociażby zjawisko gigantycznego magnetooporu (uhonorowane nagrodą Nobla w 2007r.), kwantowe efekty tunelowania, procesy zachodzące w układach spintronicznych, czy też nowe źródła anizotropii magnetycznej. Postęp technologii oraz nowe odkrycia prowadzą również do zastosowania nanoukładów w produkcji magnetycznych czujników (np. w tomografii rezonansowej) oraz systemów informacyjnych (np. w pamięciach MRAM – ang. Magnetoresistive Random Access Memory) z ciągle malejącą aktywną powierzchnią nośników oraz wzrastającą gęstością zapisu bitowego. Wytworzenie warstw o grubości kilku nanometrów nie jest możliwe bez odpowiedniego podłoża, którego wybór często decyduje o jakości tych warstw oraz ich właściwościach. W nanostrukturach magnetycznych wytwarzanych na odpowiednio „strukturyzowanych” powierzchniach schodkowych (ang. vicinal surface), w postaci tarasów rozdzielających monoatomowe schodki, występuje zmiana symetrii otoczenia jonu magnetycznego na powierzchni oraz na krawędzi schodków w porównaniu z symetrią w objętości warstwy. W przypadku podłoża schodkowego, złamanie symetrii translacji powoduje zmniejszenie koordynacji sąsiednich atomów powierzchniowych na krawędziach schodków, spowodowanej zerwaniem ich wiązań chemicznych. Naruszenie wiązań prowadzi do redukcji symetrii w ultracienkiej warstwie magnetycznej ze znaczącym wkładem powierzchniowym do anizotropii magnetycznej, zgodnie z modelem par spinowych Néel’a [11]. Założenie teoretyczne w tym modelu polegało na uwzględnieniu złamania symetrii nie tylko w kierunku prostopadłym (wzrostu), ale również równoległym w płaszczyźnie warstwy. Pierwsze eksperymentalne potwierdzenie tej magnetycznej anizotropii było uzyskane w zespole Gradmann’a w latach sześćdziesiątych XX wieku [12]. Bardzo interesującym przypadkiem modyfikacji anizotropii powierzchniowej jest możliwość indukowania strukturą schodkową dodatkowej anizotropii magnetycznej w płaszczyźnie warstwy, której istnienie po raz pierwszy było zaobserwowane około 30 lat później [13]. Przełomem w badaniach nanostruktur magnetycznych był burzliwy rozwój technologii wytwarzania ultracienkich warstw w warunkach ultrawysokiej próżni, powstaniem nowych metod charakteryzacji powierzchni oraz badań magnetycznych i magnetooptycznych. W pracach [14,15], które są często cytowane, był zaobserwowany in-situ w temperaturze 150 K wpływ podłoża schodkowego na spinową reorientację oraz anizotropię magnetyczną w układzie Fe/Ag. Zmiana krytycznej grubości tej reorientacji wynosiła najwyżej wielkość grubości jednowarstwowej, co stanowiło wzrost zaledwie o ok. 15% grubości krytycznej dla płaskiego podłoża. W układach Co/Au [16] obserwowano in-situ również niewielką zmianę zakresu spinowej reorientacji, przy czym grubość krytyczna była nawet mniejsza w porównaniu z grubością dla podłoża płaskiego. Wśród interesujących niskowymiarowych obiektów badanych należy wymienić: uzyskane samoorganizacje atomowych łańcuchów Co na podłożu schodkowym Pt [17], ultracienkie paski atomów Fe [18], matryce uporządkowanych klasterów Co [19], itd. Z przeglądu literatury, dotyczącego badań wpływu podłoża na magnetyzm nanoszonych na nie nanostruktur, można zauważyć, iż istotna część badań magnetycznych została przeprowadzona w warunkach ultawysokiej próżni, a więc in-situ, a najbardziej znaczące wyniki były uzyskane przy bezpośrednim wzroście nanostruktur magnetycznych na monokryształach, takich jak Ag, Au, Cu, Pt itp. Oczywiście takie podejście daje jakościowo dobre warunki wzrostu warstw magnetycznych, ale również stanowi szereg istotnych ograniczeń, np. w zakresie modyfikacji anizotropii magnetycznej, energii powierzchniowej, struktury krystalograficznej warstw, jak też w aplikacjach.
Wyniki
Tematyka badań obejmuje kompleksowe badania nanostruktur magnetycznych na powierzchniach ze złamaną symetrią translacyjną. Główna idea badań polegała na wykorzystaniu podłoża (Al2O3, Mo, W, Si) ze strukturą schodkową (schodki monoatomowe oraz grupy schodków) w postaci szablonu, na który przed wytworzeniem warstwy magnetycznej, nanoszona była warstwa buforowa (Mo, Cu, Au).
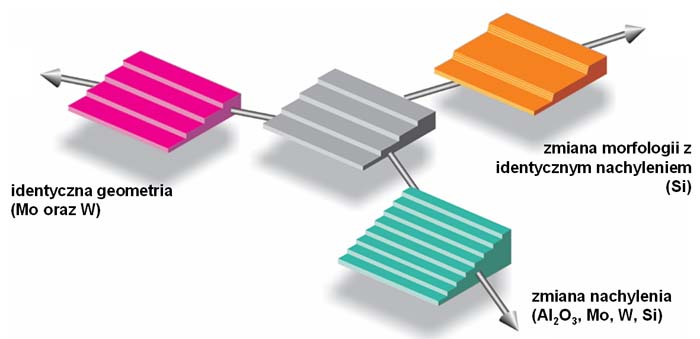
Rys. 2 Podłoża schodkowe o różnycm nachyleniu oraz morfologii
W kolejnym kroku wszystkie próbki zostały zabezpieczone (przed utlenianiem) cienką warstwą Au w celu przeprowadzenia badań ex-situ. Badane próbki zostały przygotowane z wykorzystaniem techniki epitaksji z wiązek molekularnych (MBE) w warunkach ultrawysokiej próżni (UHV). Badania powierzchni oraz parametrów strukturalnych warstw wykonano przy pomocy technik in-stu takich jak dyfrakcja elektronowa (RHEED i LEED) oraz skaningowa mikroskopia tunelowa (STM). Stwierdzono bardzo silny wpływ struktury podłoża oraz warstw buforowych na uporządkowanie magnetyczne ultracienkiej warstwy kobaltu. Główne pomiary magnetyczne i optyczne zostały przeprowadzone przy wykorzystaniu technik rezonansu ferromagnetycznego (FMR) w paśmie X, magnetometrii i mikroskopii magnetooptycznego efektu Kerra (MOKE) oraz magnetooptycznej spektroskopii generacji drugiej harmonicznej (MSHG). Główne kierunki badawcze były związane z: – modyfikacją zarówno anizotropii magnetokrystalicznej jak też i magnetycznej anizotropii indukowanej powierzchnią schodkową oraz powierzchnią warstw buforowych w układach Co/Si, Co/Au i Co/Cu,.
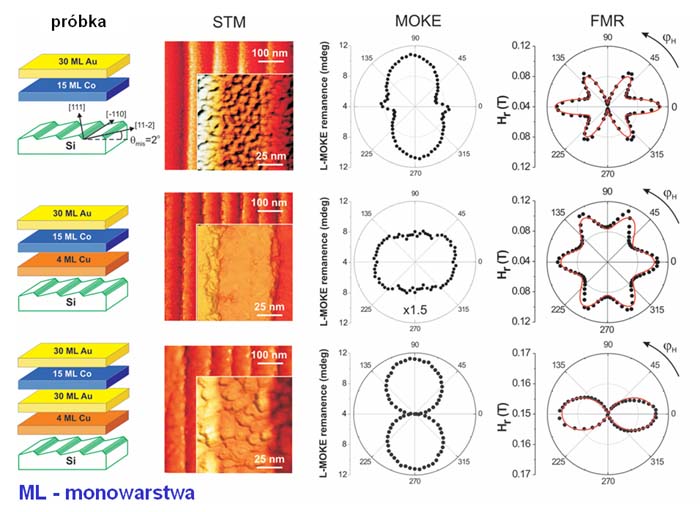
Rys. 3 Modyfikacja anizotropii magnetycznej [1,5,7]
– indukowaniem prostopadłej składowej magnetyzacji oraz spinowej reorientacji, od kierunku prostopadłego względem powierzchni warstwy do kierunku w płaszczyźnie, w szerokim zakresie (1-8 nm) grubości warstwy kobaltu oraz różnej geometrii podłoża W i Mo.
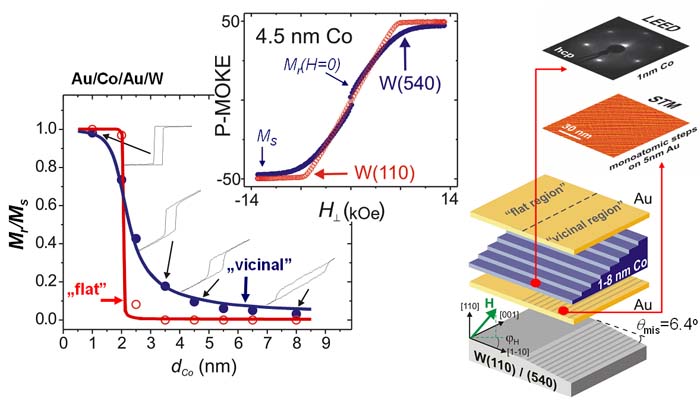
Rys. 4 Indukowanie spinowej reorientacji w nanostrukturach kobaltu [4,6]
– do opisu anizotropii magnetycznej warstw Co zaproponowano model fenomenologiczny, uwzględniający jedynie parametry magnetyczne dla warstw na referencyjnym podłożu płaskim oraz czynnik geometryczny związany z nachyleniem podłoża schodkowego,
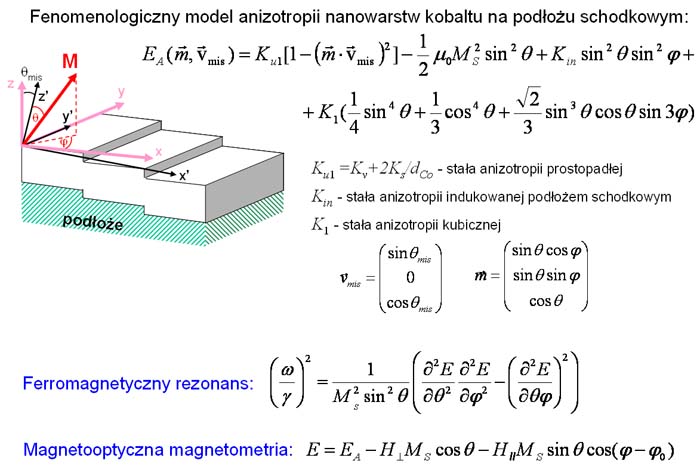
Rys. 5 Model anizotropii magnetycznej warstw Co na podłożach schodkowych [2,6,7]
– modyfikacją tensora oddziaływań wymiennych w obszarze krawędzi schodków z anizotropią dynamiki ściany domenowej. W szczególności, zaobserwowano wzrost prędkości ściany domenowej o około dwa rzędy wielkości dla warstw Au/Co/Au na podłożu Si z grupami schodków.
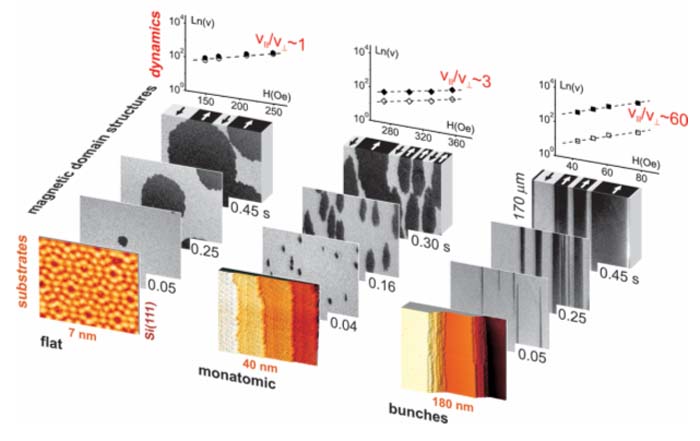
Rys. 6 Anizotropia dynamiki ściany domenowej [3,8]
– możliwość „strukturyzacji” niemagnetycznej powierzchni podłoża w celu uzyskania samoorganizacji z obniżeniem wymiarowości nanoszonych na nie obiektów magnetycznych (np. druty, klastery, kropki). W pracy [20] zaprezentowano możliwość uzyskiwania na powierzchni schodkowej Si(111) regularnych kropek kobaltowych o gęstościach do Tbit/in2 (jeżeli założymy, że odpowiednikiem kropki jest bit).
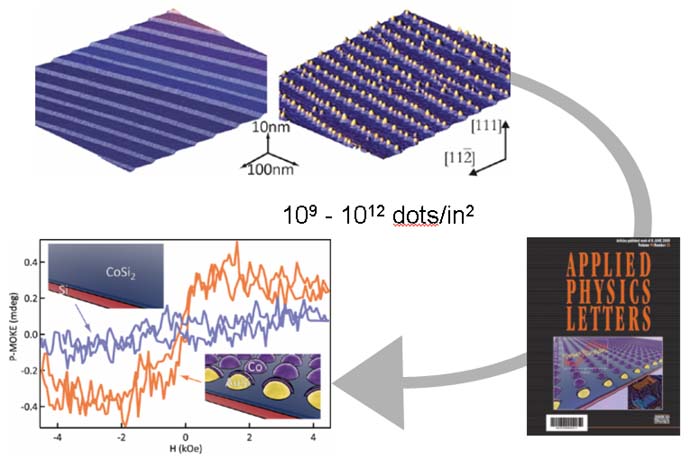
Rys. 7 Magnetyczna strukturyzacja
Podsumowanie
Uzyskane wyniki mogą być wykorzystane do tworzenia nowych systemów o zadanych właściwościach magnetycznych oraz redukcji wymiarowości w skali atomowej. Szczególnie interesujące są połączenia magnetycznych nanostruktur metalicznych z półprzewodnikowym podłożem schodkowym, które mogą być kluczem do tworzenia urządzeń spintronicznych jak również strukturyzowanych układów magnetycznych.
Literatura
- A. Stupakiewicz, Z. Kurant, A. Maziewski, L.T. Baczewski A. Maneikis, A.Wawro, J. Magn. Magn. Mater. 290-291, 242 (2005).
- A. Stupakiewicz, R. Gieniusz, A. Maziewski, K. Postava, A. Wawro, L.T. Baczewski, phys. stat. sol. (b) 243, 202 (2006).
- A. Stupakiewicz, M. Tekielak, A. Maziewski, V. Zablotskii, L.T. Baczewski, A. Wawro, J. Magn. Magn. Mater. 316, e136 (2007).
- A. Stupakiewicz, A. Maziewski, M. Ślęzak, T. Ślęzak, M. Zając, K. Matlak, J. Korecki, J. Appl. Phys. 103, 07B520 (2008).
- A. Stupakiewicz, A. Fleurence, A. Maziewski, T. Maroutian, P. Gogol, B. Bartenlian, R. Mégy, P. Beauvillain, IEEE Trans. Magn. Vol. 44, 11, 2887 (2008).
- A. Stupakiewicz, A. Maziewski, K. Matlak, N. Spiridis, M. Ślęzak, T. Ślęzak, M. Zając, J. Korecki, Phys. Rev. Lett. 101, 217202 (2008).
- A. Stupakiewicz, A. Kirilyuk, A. Fleurence, R. Gieniusz, T. Maroutian, P. Beauvillain, A. Maziewski, Th. Rasing, Phys. Rev. B 80, 094423 (2009).
- A. Stupakiewicz, E. Vedmedenko, A. Fleurence, T. Maroutian, P. Beauvillain, A. Maziewski, R. Wiesendanger, Phys. Rev. Lett. 103, 137202 (2009).
- Ultrathin Magnetic structures red. J.A.C. Bland and B. Heinrich, Springer, Berlin, 1994
- F.J. Himpsel, J.E. Ortega, G.J. Mankey, R.F. Willis, Advances in Physics 47, 511 (1998).
- L. Néel, J. Phys. Rad. 15, 225 (1954).
- U. Gradmann, J. Müller, Phys. Status Solidi 27, 313 (1968).
- B. Heinrich, S.T. Purcell, J.R. Dutcher, K.B. Urquhart, J.F. Cochran, A.S. Arrott, Phys. Rev. B 38, 12879 (1988).
- R.K. Kawakami, E.J. Escorcia-Aparicio, Z.Q. Qiu, Phys. Rev. Lett. 77, 2570 (1996).
- R.K. Kawakami, M.O. Bowen, H.J. Choi, E.J. Escorcia-Aparicio, and Z.Q. Qiu, Phys. Rev. B 58, R5924 (1998).
- G. Rodary, V. Repain, R.L. Stamps, Y. Girard, S. Rohart, A. Tejeda, and S. Rousset, Phys. Rev. B 75, 184415 (2007).
- P. Gambardella, A. Dallmeyer, K. Maiti, M. C. Malagoli, W. Eberhardt, K. Kern, and C. Carbone, Nature, 416, 301 (2002).
- O. Pietzsch, A. Kubetzka, M. Bode, and R.Wiesendanger, Phys. Rev. Lett. 84, 5212 (2000).
- S. Rousset, V. Repain, G. Baudot, Y. Garreau, and J Lecoeur, J. Phys.: Condens. Matter 15, S3363 (2003).
- E. Moyen, M. Macé, G. Agnus, A. Fleurence, T. Maroutian, F. Houzé, A.Stupakiewicz, L. Masson, B. Bartenlian, W. Wulfhekel, P. Beauvillain and M. Hanbücken, Appl. Phys. Lett., 94, 233101 (2009).
