Proces magnesowania oraz struktury domenowe w kobaltowych mikrodrutach
Wstęp
Badania właściwości fizycznych drutów ferromagnetycznych są związane ze zrozumieniem zjawisk zachodzących w obiektach jednowymiarowych [1], jak również coraz większą liczbą możliwości aplikacyjnych [2]. Kontrola na poziomie anizotropii oraz stanów magnetyzacji może być realizowana przy pomocy odpowiednich drutów magnetycznych o rozmiarach mikronowych lub submikronowych, które są wykorzystane obecnie w zaawansowanych czujnikach oraz różnorodnych aplikacjach biomedycznych [2,4]. Rola anizotropii magnetycznej dla układów mikromagnetyków jest bardzo ważna. Między innymi amorficzne druty ferromagnetyczne w obecność kształtu osiowego oraz cyrkularnego wykazują różnorodność struktur domenowych oraz różnych faz magnetycznych. Jest to związane z konkurencją różnych wkładów anizotropii (osiowy, radialny oraz powierzchniowy), które są skutkiem naprężeń wewnętrznych zależnych od izolacji termicznej i/lub mechanicznej historii drutu. A więc w takim drucie rzeczywisty rozkład indukowanej anizotropii magnetycznej jest określany przez rozkład naprężeń, jak również poprzez znak i amplitudę magnetostrykcji. Na przykład, dla drutów z negatywną magnetostrykcją w rdzeniu dominuje anizotropowy wkład osiowy, natomiast shell pozwala zaindukować anizotropię o charakterze helikoidalnym. W takich drutach obserwuje się zarówno osiowy kierunek magnetyzacji jak również radialny.
Wyniki badań
Intensywne badania właściwości magnetycznych (z praktycznie zerową magnetostrykcją) kobaltowych mikrodrutów amorficznych jest związane z odkryciem w tych materiałach efektu gigantycznej magnetoinpedacji. Z drugiej strony mikrodruty również mogą być wykorzystane do badań jako system modelowy jednowymiarowych nanostruktur magnetycznych.
Do badania procesu magnesowania wykorzystano technikę magnetooptycznego efektu Kerra (MOKE) w konfiguracji poprzecznej. Natomiast badanie struktur domenowych przeprowadzono przy zastosowaniu układu optycznej mikroskopii MOKE w konfiguracji podłużnej. Jako zewnętrzne pola magnetyczne zastosowano magnetyczne pole przyłożone osiowo HAX oraz pole syrkularne Hcir wytworzone przy pomocy prądu elektrycznego I.
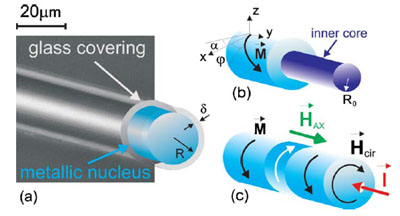
Obraz (a) oraz schematyczna konfiguracja (b) drutu z zaznaczonym kierunkiem magnetyzacji, schemat (c) nukleacji struktury domenowej oraz orietacji pola magnetycznego.
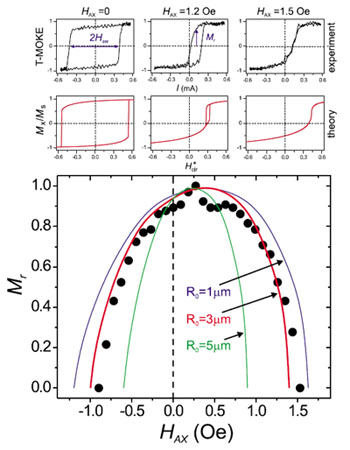
Górny panel: krzywe magnesowania oraz wyniki symulacji zależności Mx/Ms w funkcji cyrkularnego pola zgodnie ze wzorem Eq.1 [6] dla Hax =0, 1.2, i 1.5 Oe. Zależność znormalizowanej pozostałości magnetycznej (remanencji) w funkcji zewnętrznego magnetycznego pola osiowego Hax (punkty). Linii są wynikiem obliczeń Mr w ramach zaproponowanego modelu anizotropii [6].
Badano proces magnesowania dla słabego pola osiowego przy zwiększeniu amplitudy prądu elektrycznego (magnetycznego pola cyrkularnego). Proces przebiegał od stanu początkowego z lewoskrętną cyrkularną orientacją magnetyzacji w następującej kolejności: (i) najpierw monotoniczna transformacja do struktury helikoidalnej, (ii) następnie skok do stanu z odwrotnym kierunkiem skrętności ze stanem helikoidalnym oraz (iii) stopniowe skręcenie wektora magnetyzacji do stanu z prawoskrętną orientacją cyrkularną [6]. Warto podkreślić, iż zewnętrzne magnetyczne pole osiowe w pewien sposób wygładza skok pomiędzy stanami z odwróconą skrętnością prowadząc do uzyskania asymetrii stanów namagnesowania w badanych drutach.
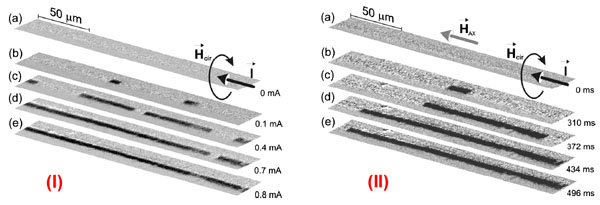
Obrazy zmiany cyrlularnej struktury domenowej w funkcji amplitudy przyłożonego prądu elektrycznego (I) oraz w obecności pola osiowego HAX=0.27Oe w funkcji czasu dla stałej amplitudy prądu (II) [5].
Wykorzystanie zewnętrznego pola magnetycznego przyłożonego w osi badanego drutu magnetycznego pozwoliło dokonać jego przemagnesowania. Ten proces jest realizowany w formie ostrych gigantycznych skoków Barkhausena [5]. Obserwowane skoki związane z szybkim ruchem pojedynczej ściany domenowej w zakresie dużych odległości rzędu 100 mikrometrów.
Literatura
A. Masseboeuf, O. Fruchart, J. C. Toussaint, E. Kritsikis, L. Buda-Prejbeanu, F. Cheynis, P. Bayle-Guillemaud, and A.Marty, Phys. Rev. Lett. 104, 127204 (2010).
M. Vázquez and A. Hernando, J. Phys. D: Appl. Phys. 29, 939 (1996).
A. Hultgren, M. Tanase, C. S. Chen, G. J. Meyer, and D. H. Reich, J. Appl. Phys. 93, 7554 (2003).
4D. S. Choi, J. Park, S. Kim, D. H. Gracias, M. K. Cho, Y. K. Kim, A. Fung, S. E. Lee, Y. Chen, S. Khanal, S. Baral, and J.-H. Kim, J. Nanosci. Nanotechnol. 8, 2323 (2008).
A. Chizhik, A. Stupakiewicz, A. Maziewski, A. Zhukov, J. Gonzalez, and J. M. Blanco, Appl. Phys. Lett. 97, 012502 (2010).
A. Chizhik, V. Zablotskii, A. Stupakiewicz, C. Gómez-Polo A. Maziewski, A. Zhukov, J. Gonzalez, J.M. Blanco, Phys. Rev. B 82, 212401 (2010).
