|
|
|
|
|
|
|
Badanie efektu Faradaya (wyznaczanie kata skręcenia płaszczyzny polaryzacji w polu magnetycznym)
Przechodząc przez domeny magnetyczne płaszczyzna liniowo spolaryzowanego światła ulega skręceniu o kąt +fi lub -fi Jeżeli wiązka światła przechodzi przez obszar zawierający wiele domen wówczas płaszczyzna polaryzacji ulega skręceniu o kąt średni <fisr>(H) proporcjonalny do m znormalizowanej magnetyzacji próbki:
<fisr>(H) =fi*m(H)
gdzie <fisr> i m zależą od pola magnetycznego H jakie przyłożone jest do próbki (przykładowa zależność m(H) przedstawiona jest na rysunku 1) Z rysunku 1 wynika, że przykładając pole H o amplitudzie większej niż Hs (około 6000 [A/m]) próbka jest całkowicie nasycona, gdy :
- H>Hs, m(H) =1, <fisr>(H)=fi;
- H<-Hs, m(H)=-1, <fisr>=-fi.
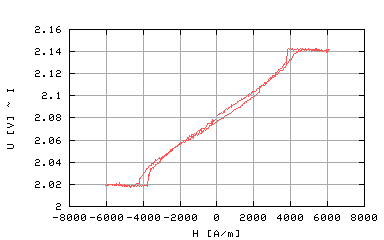
Rysunek 1: Przykładowa zależność m(H)
W celu wyznaczenia kąta fi korzysta się z prawa Malusa wiążącego natężenie I liniowo spolaryzowanego światła przechodzącego przez polaryzator wzorem:
I= I0 Cos2(delta)
gdzie I0 jest natężeniem wiązki padającego światła, delta kątem pomiędzy płaszczyzną polaryzacji a osią przepuszczania polaryzatora.
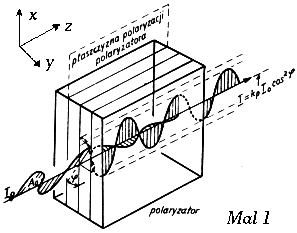
Rysunek 2: Ilustracja liniowo spolaryzowanego światła przechodzącego przez polaryzator.
Proponuje się wykonać "Pomiar natężenia światła w funkcji położenia polaryzatora i natężenia pola magnetycznego" w dwóch przypadkach gdy próbka jest nasycona H>Hs i H<-Hs (np. H=6000 i H=-6000 [A/m]). Wówczas, korzystając z prawa Malusa natężenia I1 i I2 w tych przypadkach opisuje się odpowiednio wzorami:
I1(alfa1)=I0Cos2(alfa1+fi) (1a)i
I2(alfa1)=I0Cos2(alfa1-fi) (1b)
gdzie alfa1 określa położenie polaryzatora. Wynikiem każdego z tych pomiarów są odpowiadające sobie dwa ciągi U(i) i alfa1(i) (1<i<N, w naszym eksperymencie N=200). U(i) jest wartością napięcia mierzonego przez detektor światła, U(i) jest mierzone w woltach, wiąże się z natężeniem światła liniową relacją:
U=a+b*I (2)
Po zakończonym pomiarze komputer standardowo wykreśla zależność U(alfa1), przykładowa prezentacja wyników widoczna jest na rysunku 3. Problem wyznaczenie kąta fi można sprowadzić do zadania określenia różnicy fazy funkcji I1(alfa1) i I2(alfa1), różnicy położenia minimów tych funkcji. Jak widać z podanych wyżej wzorów (1) na I1 i I2, różnica ta wynosi 2*fi.
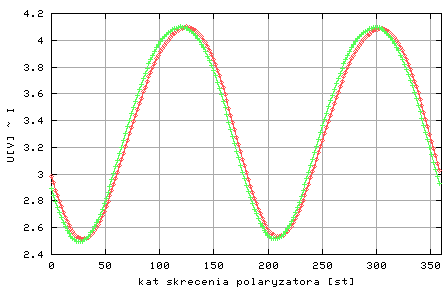
Rysunek 3: Wynik pomiarów natężenia światła w funkcji kąta alfa1. Detektor zarejestrował sygnał U1(alfa1) i U2(alfa1) przy nasycenia próbki polem magnetycznym odpowiednio H=6000[A/m] i H=-6000 [A/m].
Jak widać z rysunku 3 zależność napięcia U(i) zmierzonego (dla dowolnej wartości pola H ) w funkcji kąta alfa1 można opisać wzorem:
U=U1+U0*cos2(alfa1+gamma).
Gdzie parametry U1, U0, gamma zależą od ustawienia polaryzatora, wartoćci pola magnetycznego oraz od kąta fi. Parametry te można dopasować korzystając z procedury zaproponowanej na stronach Sprawdzanie prawa Malusa. Dalej analizowana jest metoda poszukiwania minimow funkcji U(alfa1).
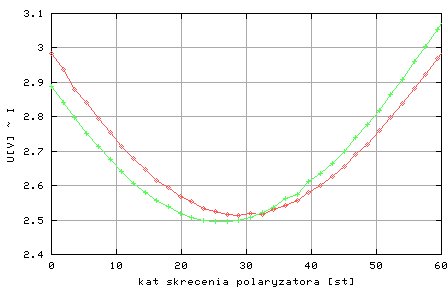
Rysunek4: Wynik pomiarów natężenia światła (dane z rysunku 3 wykreślone w mniejszym zakresie kąta alfa1)
Na rysunku 4 przedstawione są zmierzone wartości U1(alfa1) i U2(alfa1) w mniejszym zakresie kątów alfa1. Bezpośrednio z takiego rysunku (pliku z danymi) możemy odczytać wartość kąta dla którego natężenie światła przyjmuje wartość mininimalną Imin dla obu pomiarów. Różnica kątów dla Imin(H+) i Imin(H-) jest równa 2*fi. Inną metodą wyznaczenia Imin jest wyliczenie różnicy dI(i) = I(i+1)- I(i) dzięki czemu można określić minimum jako punkt dla którego wartość bezwzględna |dI| jest najmniejsza. Wybieramy więc zakres danych z okolicy minimum sygnału w zakresie +/- 15-20 stopni i wykonujemy różnicowanie. Otrzymany wynik przybliżamy następnie linią prostą co pozwoli nam na znalezienie wartości kąta dla którego różnica dI przyjmuje wartość 0. W tym celu korzystamy z GnuPlota. Dopasowywać będziemy funkcją typu dI(i) = A *delta +B (1) parametry A i B szacujemu z wykresu. A - jest nachyleniem prostej ( współczynnik kierunkowy) B -miejscem przecięcia z osią 0Y. W naszym przypadku oszacujemy A = 0.002 i B= -0.06. następnie poleceniem wydając w GnuPlot-cie polecenia:
A1 = 0.002
B1 = -0.06
fun(x) =A1*x+B1
fit fun(x) "wyn-mino.dat" via A1,B1
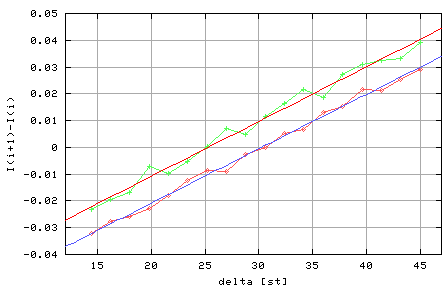
Rysunek4: Wynik dopasowania różnicy I(i+1)-I(i) linią prostą dla przypadków nasycenia polem Hs i -Hs
Korzystając ze znalezionych parametrów dopasowania wyznaczamy miejsce przecięcia z osią OX dla obu zmierzonych przypadków ( z namagnesowaniem Hs i -Hs). Dokonujemy tego podstawiając liczbowe wartości A i B do równania (1) i rozwiązując je ze względu na x po przyrównaniu całośći do zera. Po wyznaczeniu obu punktów przecięcia z osią OX wyliczamy kąt skręcenia Faradaya jako fi = (delta0- -delta0+)/2 (gdzie delta0 - kąt dla którego I(i+1)-I(i) = 0)
Dodatkowo:
Program w języku C do różnicowania danych
|
|
| Laboratory of Magnetism, Faculty of Physics, University of Białystok |
| Białystok Branch Polish Physical Society, |
| Ciołkowskiego 1L, 15-245 Białystok 15-424, Poland, E-mail: dobrog@uwb.edu.pl WWW: http://labfiz.uwb.edu.pl/exp/domeny01/ |
| Last modification: October 17, 2019 |