
Wynik w postaci wykresu natężenia światła w funkcji kąta rozkrzyżowania polaryzatorów - przykład uruchomienia programu pomiarowego w doświadczeniu 1 z domyślnymi parametrami startowymi.
Celem doświadczenia jest pomiar natężenia światła I w funkcji kąta alfa pomiędzy płaszczyznami głównymi polaryzatora 1 i polaryzatora 2. Doświadczenie można wykonac dla określonej przez Internautę wartości pola magnetycznego H przykładanego prostopadle do powierzchni badanej warstwy. Na stronach WWW przedstawiony jest układ pomiarowy oraz konfiguracja pola i próbki.
Korzystajac z prawa Malusa można opisac natężenie światła padającego na detektor wzorem:
I(H)= I0 Cos2 (alfa+fisr(H))
gdzie alfa jest kątem pomiędzy płaszczyznami głównymi polaryzatora 1 i polaryzatora 2, a fisr - katem skręceniia płaszczyzny polaryzacji światła przechodzącego przez próbkę. fisr zależy od znormalizowanej magnetyzacji próbki m(H) zgodnie ze wzorem:
fisr = fi* m(H)
Zakładamy, że napięcie U rejestrowane przez edtektor liniowo zależy od natężenia padającego na niego światła. Można wówczas zapisać U w postaci:
U(alfa)= A+C Cos2(alfa+fisr)
Doświadczenie wykonuje się w funkcji kąta alfa1=(alfa-alfa0) opisującego położenie płaszczyzny głównej polaryzatora, alfa1 jest określany względem dowolnej osi. '; // --------------------------------------------------- soft $soft='
Program wykonujący pomiar w tym doświadczeniu bazuje na wykorzystaniu technologi CGI. Dzięki temu istnieje możliwość uruchomienia podprogramów sterujących układem i zbierających z dane. Parametry uruchomieniowe skryptu CGi do pomiaru natężenia światła w funkcji położenia polaryzatora i natężenia to:
Uruchomienie pomiaru następuje po naciśnięciu przycisku "Uruchom". Przekroczenie zakresu któregoś z parametrów jest sygnalizowane, a program ustawia przekroczony parametr na wartość domyślna jednocześnie zgłaszając który z parametrów został niepoprawnie wpisany. Tym samym program jest zabezpieczony przed wstawianiem niepoprawnych wartości. Po wykonaniu pomiaru dane są przedstawione w postaci wykresu - pliku graficznego w formacie PNG otrzymanego jako wynik działania programu Gnuplot. Zachowanie tego pliku jest możliwe poprzez standardową funkcję przeglądarki jaką jest "Save Image as..", a która kryje się pod prawym klawiszem myszy w momencie naciśnięcia go gdy kursor myszy znajduje sie "ponad" obrazem. Dostęp do danych pomiarowych uzyskanych w doświadczeniu jest możliwy także w formie tekstowej. Pod przyciskiem "Zobacz/Zapisz dane" który pojawia się po wykonaniu pomiaru kryje się nowe okienko przeglądarki w którym możemy zobaczyć dane w postaci tabeli i mamy możliwość zapisania ich na lokalny dysk. Zamknięcie okienka z danymi odbywa się po naciśnięciu przycisku "Zamknij". W pliku z danymi poza informacją na temat kąta, odpowiadającemu temu kątowi napięcia i błedu pomiaru napięcia które umieszczone są w kolumnach, zawarta jest też informacja na temat parametrów pomiaru i daty jego wykonania. Opis działania programu znajduje się pod przyciskiem "Pomoc". Polecam korzystanie z tej mozliwości w razie niejasności .

Wynik w postaci wykresu natężenia światła w funkcji kąta rozkrzyżowania polaryzatorów - przykład uruchomienia programu pomiarowego w doświadczeniu 1 z domyślnymi parametrami startowymi.
Po przesłaniu parametrów uruchomieniowych ze strony WWW (skryptu CGI) do podprogramu na komputerze pomiarowym następuje wykonanie poniższego algorytmu pomiarowego:
Wynik pomiaru jest zapisywany do pliku który dostępny jest programowi CGI i na podstawie którego tworzony jest wykres wyświetlany później w przeglądarce. Na stronie poświęconej opisowi układu pomiarowego można znaleźć bliższe informacje na temat sterowania położeniem polaryzatora, natęzeniem pola magnetycznego i pomiaru natężenia światła w naszym układzie. '; // ----------------------------------------------------------------- Malus $malus=' Sprawdzanie prawa Malusa
Wizualizacja domen magnetycznych w naszym zestawie pomiarowym wymaga stosowania układu polaryzator - analizator. Zestaw umożliwia również zmianę kąta alfa pomiędzy osią maksymalnego przepuszczania polaryzatora i analizatora. Taka konfiguracja, poza głównym celem jakim jest badanie domen, umożliwia więc także przeprowadzenie doświadczenia którego celem jest potwierdzenie prawa Malusa.
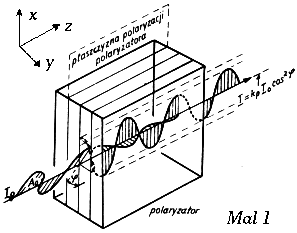
Na rysunku obok mamy schematycznie przedstawioną liniowo spolaryzowaną falę elektromagnetyczną przechodzącą przez polaryzator. Padająca fala zostaje częściowo wygaszona - przechodzi jedynie składowa amplitudy fal (wektora elektrycznego E) równoległa do płaszczyzny głownej polaryzatora (na rysunku m1 oś x). Zmianę natężenia światła można łatwo wyprowadzić rzutując wektor elektryczny E na oś przepuszczania i zakładając proporcjonalność I do kwadratu E.
I(delta)=I0 Cos2(delta)
gdzie I0 - natężenie światła padającego na polaryzator, delta - kąt pomiędzy płaszczyzną polaryzacji i osia przepuszczania polaryzatora
Tego typu związek został sformułowany już w 1810 roku przez Malusa i jest nazywany obecnie prawem Malusa.
W naszym eksperymencie możemy mierzyć natężenie I(alfa H) w funkcji kąta alfa (kąt pomiędzy płaszczyznami głownymi polaryzatora 1 i polaryzatora 2) i natężenia pola magnetycznego H przykładanego do próbki. Korzystając z prawa Malusa I można zapisać jako:
I(alfa)=I0 Cos2(alfa +fisr)
gdzie fisr - jest kątem skręcenia płaszczyzny polaryzacji światła przechodzącego przez próbkę. fisr zależy od magnetyzacji próbki m, którą możemy zmienić regulując wartość pola H; fisr = fi * m(H)
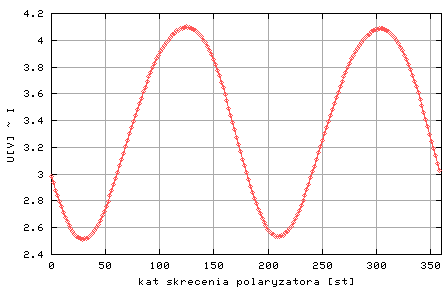
Rysunek Mal2:Przykładowy wynik pomiarów natężenia światła przechodzącego przez próbkę magnetyczną w funkcji kąta położenia polaryzatora alfa 1 =(alfa +alfa 0)
Wykonanie pomiaru
W celu wykonania pomiaru należy uruchomić program sterujący doświadczeniem: "Pomiar natężenia światła w funkcji położenia polaryzatora i natężenia pola magnetycznego", a następnie wykonać pomiar przy dowolnie ustawionej wartości amplitudy pola magnetycznego (np 0 [A/m]). Wynikiem pomiaru są odpowiadające sobie dwa ciągi U(i) i alfa1(i) (1 <i <N, w naszym eksperymencie N=200). U(i) jest wartością napięcia mierzonego przez detektor światła (wartością podawaną w woltach) i wiąże się z natężeniem światła I liniową relacją:
U = a+b*I
alfa1(i) określa położenie polaryzatora, w którym dokonano pomiaru U(i).
Po zakończonym pomiarze komputer standardowo wykreśla zależność U(alfa1), Przykładowa prezentacja wyników widoczna jest na rysunku Mal 2. Na stronie Pomiar natężenia światła w funkcji położenia polaryzatora i natężenia pola magnetycznego istnieją jeszcze dwie dodatkowe opcje zapoznania się z uzyskanymi wynikami :
Sprawdzenia prawa Malusa mozemy dokonać porównując zmierzone wartości U(alfa1(i)) z wartościami teoretycznymi UT(alfa1(i)) wyliczonymi ze wzoru:
UT(alfa1) =a +b0 * Cos2(alfa1+alfa0)
Problem sprowadza się do znalezienia trzech parametrów U1, U0 i alfa0 by zależność teoretyczna UT(alfa1) jak najlepiej opisywała wyniki przeprowadzonego doswiadczenia. Do oszacowania tych parametrów można zwrócić uwagę na maksymalne i minimalne wartości U:
W celu precyzyjnego określenia (dopasowania - "dofitowania" od angielskiego słowa "fitting") parametrów U1, U0 i alfa0 poszukuje się minimum sumy (U(alfa(i)) -UT(alfa(i)))2. Istnieją specjalne metody numeryczne pozwalające na znalezienie tego minimum. Dalej proponowane jest wykorzystanie w tym celu bezpłatnie dostępnego programu GnuPlot Na rysunku Mal 3 widać, że dopasowana krzywa teoretyczna nieźle opisuje wyniki doświadczalne.
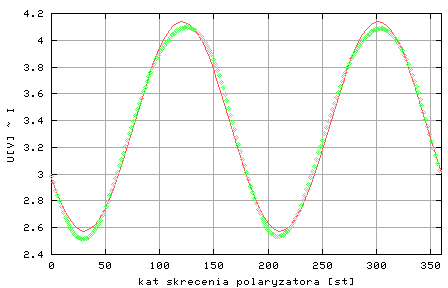
Rysunek Mal 3 : Uzyskana z prawa Malusa krzywa teoretyczna (linia ciagła) dopasowana do wyników eksperymentalnych.
Przykładowy program w języku programu Gnuplot do dopasowania naszych wyników:
set angles degrees
fun(alfa1) = a + b0*cos(alfa1+alfa0 )**2
fit fun(alfa1) "dane.dat" via "par.dat"
Polecenie set angles degrees określa sposób zapisywania kątów ( w stopniach nie w radianach które są domyślne dla większości programów komputerowych). Postać funkcji uwzględnia takie parametry jak: przesunięcie poziomu sygnału - U1, skalowanie funkcji cos - U0 i przesunięcie fazy - parametr alfa1. Kolejna linia wywołuje dopasowanie "fit" które do danych zawartych w pliku dane.dat dopasowuje funkcję fun(alfa1). Plik par.dat spis początkowych wartości parametrów użytych wfunkcji fun(x).
a = 2.6
b0 = 1.4
alfa0 =-60
Program gnuplot można ściągnąć spod tego adresu: http://www.gnuplot.org '; // ------------------------------------------------- Faraday $faraday='
Badanie efektu Faradaya (wyznaczanie kata skręcenia płaszczyzny polaryzacji w polu magnetycznym)
Przechodząc przez domeny magnetyczne płaszczyzna liniowo spolaryzowanego światła ulega skręceniu o kąt +fi lub -fi Jeżeli wiązka światła przechodzi przez obszar zawierający wiele domen wówczas płaszczyzna polaryzacji ulega skręceniu o kąt średni <fisr>(H) proporcjonalny do m znormalizowanej magnetyzacji próbki:
<fisr>(H) =fi*m(H)
gdzie <fisr> i m zależą od pola magnetycznego H jakie przyłożone jest do próbki (przykładowa zależność m(H) przedstawiona jest na rysunku 1) Z rysunku 1 wynika, że przykładając pole H o amplitudzie większej niż Hs (około 6000 [A/m]) próbka jest całkowicie nasycona, gdy :
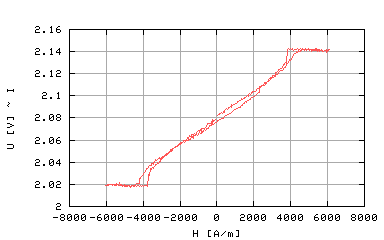
Rysunek 1: Przykładowa zależność m(H)
W celu wyznaczenia kąta fi korzysta się z prawa Malusa wiążącego natężenie I liniowo spolaryzowanego światła przechodzącego przez polaryzator wzorem:
I= I0 Cos2(delta)
gdzie I0 jest natężeniem wiązki padającego światła, delta kątem pomiędzy płaszczyzną polaryzacji a osią przepuszczania polaryzatora.

Rysunek 2: Ilustracja liniowo spolaryzowanego światła przechodzącego przez polaryzator.
Proponuje się wykonać "Pomiar natężenia światła w funkcji położenia polaryzatora i natężenia pola magnetycznego" w dwóch przypadkach gdy próbka jest nasycona H>Hs i H<-Hs (np. H=6000 i H=-6000 [A/m]). Wówczas, korzystając z prawa Malusa natężenia I1 i I2 w tych przypadkach opisuje się odpowiednio wzorami:
I1(alfa1)=I0Cos2(alfa1+fi) (1a)i
I2(alfa1)=I0Cos2(alfa1-fi) (1b)
gdzie alfa1 określa położenie polaryzatora. Wynikiem każdego z tych pomiarów są odpowiadające sobie dwa ciągi U(i) i alfa1(i) (1<i<N, w naszym eksperymencie N=200). U(i) jest wartością napięcia mierzonego przez detektor światła, U(i) jest mierzone w woltach, wiąże się z natężeniem światła liniową relacją:
U=a+b*I (2)
Po zakończonym pomiarze komputer standardowo wykreśla zależność U(alfa1), przykładowa prezentacja wyników widoczna jest na rysunku 3. Problem wyznaczenie kąta fi można sprowadzić do zadania określenia różnicy fazy funkcji I1(alfa1) i I2(alfa1), różnicy położenia minimów tych funkcji. Jak widać z podanych wyżej wzorów (1) na I1 i I2, różnica ta wynosi 2*fi.
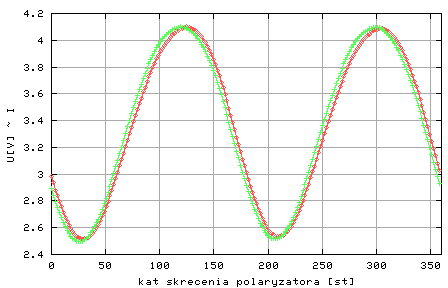
Rysunek 3: Wynik pomiarów natężenia światła w funkcji kąta alfa1. Detektor zarejestrował sygnał U1(alfa1) i U2(alfa1) przy nasycenia próbki polem magnetycznym odpowiednio H=6000[A/m] i H=-6000 [A/m].
Jak widać z rysunku 3 zależność napięcia U(i) zmierzonego (dla dowolnej wartości pola H ) w funkcji kąta alfa1 można opisać wzorem:
U=U1+U0*cos2(alfa1+gamma).
Gdzie parametry U1, U0, gamma zależą od ustawienia polaryzatora, wartoćci pola magnetycznego oraz od kąta fi. Parametry te można dopasować korzystając z procedury zaproponowanej na stronach Sprawdzanie prawa Malusa. Dalej analizowana jest metoda poszukiwania minimow funkcji U(alfa1).
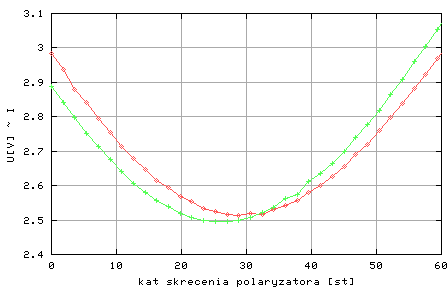
Rysunek4: Wynik pomiarów natężenia światła (dane z rysunku 3 wykreślone w mniejszym zakresie kąta alfa1)
Na rysunku 4 przedstawione są zmierzone wartości U1(alfa1) i U2(alfa1) w mniejszym zakresie kątów alfa1. Bezpośrednio z takiego rysunku (pliku z danymi) możemy odczytać wartość kąta dla którego natężenie światła przyjmuje wartość mininimalną Imin dla obu pomiarów. Różnica kątów dla Imin(H+) i Imin(H-) jest równa 2*fi. Inną metodą wyznaczenia Imin jest wyliczenie różnicy dI(i) = I(i+1)- I(i) dzięki czemu można określić minimum jako punkt dla którego wartość bezwzględna |dI| jest najmniejsza. Wybieramy więc zakres danych z okolicy minimum sygnału w zakresie +/- 15-20 stopni i wykonujemy różnicowanie. Otrzymany wynik przybliżamy następnie linią prostą co pozwoli nam na znalezienie wartości kąta dla którego różnica dI przyjmuje wartość 0. W tym celu korzystamy z GnuPlota. Dopasowywać będziemy funkcją typu dI(i) = A *delta +B (1) parametry A i B szacujemu z wykresu. A - jest nachyleniem prostej ( współczynnik kierunkowy) B -miejscem przecięcia z osią 0Y. W naszym przypadku oszacujemy A = 0.002 i B= -0.06. następnie poleceniem wydając w GnuPlot-cie polecenia:
A1 = 0.002
B1 = -0.06
fun(x) =A1*x+B1
fit fun(x) "wyn-mino.dat" via A1,B1

Rysunek4: Wynik dopasowania różnicy I(i+1)-I(i) linią prostą dla przypadków nasycenia polem Hs i -Hs
Korzystając ze znalezionych parametrów dopasowania wyznaczamy miejsce przecięcia z osią OX dla obu zmierzonych przypadków ( z namagnesowaniem Hs i -Hs). Dokonujemy tego podstawiając liczbowe wartości A i B do równania (1) i rozwiązując je ze względu na x po przyrównaniu całośći do zera. Po wyznaczeniu obu punktów przecięcia z osią OX wyliczamy kąt skręcenia Faradaya jako fi = (delta0- -delta0+)/2 (gdzie delta0 - kąt dla którego I(i+1)-I(i) = 0)
Dodatkowo:
Program w języku C do różnicowania danych
';
// ---------------------------------------------- petla wykonawcza
switch ($GLOBALS[tr]) {
case 'fizyka':
$tresc=$fizyka;
break;
case 'soft':
$tresc=$soft;
break;
case 'pomiar':
$tresc=$pomiar;
break;
case 'malus':
$tresc=$malus;
break;
case 'faraday':
$tresc=$faraday;
break;
default:
$tresc=$home;
}
// --------------------------------------------------- Szkielet
print '
Pomoc
Pomiar natężenia światła w funkcji położenia polaryzatora i
natężenia pola magnetycznego
';
print_stopka("help_dosw_1.php",$lang); ?>
'.$menu.'
'.$tresc.'