zdefiniowanej przez wyrażenie całkowe:
I. Wstęp
W wykładzie tym przedstawiłem aktualny stan wiedzy oraz zarysowałem perspektywy na najbliższe lata w dziedzinie, której wspólnym mianownikiem jest wykorzystanie femtosekundowych impulsów promieniowania laserowego. Niestety ograniczony czas wykładu nie pozwolił na dokonanie pełnego przeglądu - ograniczyłem się zatem do zilustrowania najważniejszych tendencji przy pomocy wybranych przykładów. Wybór taki jest, w pewnej mierze, podyktowany moimi upodobaniami i dlatego mój wykład nie może pretendować do miana w pełni obiektywnego przeglądu osiągnięć w omawianej dziedzinie. Optyczne techniki i technologie femtosekundowe zostały wynalezione i rozwinięte przez fizyków niejako “przy okazji” badań nad laserami. Nie powinno zatem budzić zdziwienia, że również pierwsze zastosowania tych technik miały miejsce w fizyce. Ultrakrótkie impulsy laserowe służą tam, z jednej strony, do badań dynamiki np., różnych procesów w cząsteczkach, wewnątrzpasmowej relaksacji nośników w ciele stałym, itp., z drugiej zaś, po wzmocnieniu mogą być użyte do jonizacji tarcz różnego rodzaju, generacji spójnego promieniowania X czy też zapłonu kontrolowanej syntezy termojądrowej. Wszakże szybko okazało się, że narzędzie wymyślone przez fizyków jest niezwykle użyteczne także w innych dziedzinach nauki i techniki, np. elementarne procesy o fundamentalnym znaczeniu w chemii czy biologii zachodzą w czasach rzędu kilkudziesięciu czy kilkuset femtosekund i ich dynamika może być z powodzeniem badana przy pomocy optycznych technik femtosekundowych. W tej chwili zdecydowana większość femtosekundowych układów laserowych instalowana jest w instytucjach badawczych, które niekoniecznie mają wiele wspólnego z fizyką.
Wykład rozpoczął się od krótkiego wprowadzenia do technik wytwarzania i charakteryzacji femtosekundowych impulsów laserowych. Szczególnie w dziedzinie charakteryzacji impulsów postęp w ostatnich latach jest olbrzymi i wymaga krótkiego przynajmniej podsumowania. Następnie przedstawiłem trzy przykłady zastosowań technik femtosekundowych do badań odpowiednio w fizyce, chemii i biologii. Ze względu na ograniczony czas wykładu niemożliwa jest choćby pobieżna prezentacja innych dziedzin; dlatego np. nie mówiłem o wykorzystaniu ultrakrótkich impulsów laserowych w telekomunikacji optycznej czy też diagnostyce medycznej.
II. Wytwarzanie i diagnostyka femtosekundowych impulsów światła
W ostatnich kilku latach postęp w dziedzinie generacji ultrakrótkich impulsów promieniowania elektro-magnetycznego zmierza w dwóch kierunkach. Celem jest, z jednej strony, uzyskanie coraz krótszych impulsów laserowych, z drugiej zaś opanowanie nowych technik wytwarzania ultrakrótkich impulsów w obszarze ultrafioletu, podczerwieni i mikrofal. Techniki generacji ultrakrótkich impulsów światła oparte na synchronizacji modów w laserze, generacji wyższych harmonicznych i procesach parametrycznych zostały szczegółowo omówione w artykule przeglądowym [1] w Postępach Fizyki, do którego odsyłamy zainteresowanych czytelników. Warto tylko dodać, że w minionym roku padł kolejny rekord – wprost z lasera szafirowego uzyskano impulsy o czasie trwania krótszym niż 5 fs [2] (1 fs = 10-15 s).
Niezwykle szybki postęp obserwujemy w dziedzinie diagnostyki (charakteryzacji)
ultra-krótkich impulsów laserowych. O ile w przeszłości na ogół wystarczyło
wiedzieć, że wytwarzany impuls jest odpowiednio
krótki, to współczesne, bardziej wyrafinowane zastosowania wymagają często
pełnej charakteryzacji impulsu. W prostszych zastosowaniach femtosekundowych
impulsów laserowych ważne jest tylko by czas trwania impulsu był odpowiednio
mały – chcemy mieć bardzo szybką lampę błyskową. Wtedy w zupełności wystarcza
standardowa diagnostyka tzn. pomiar funkcji autokorelacji natężeniowej
zdefiniowanej przez wyrażenie całkowe:
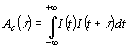(1)
oznacza zależne od czasu natężenie światła w impulsie. Mając zmierzoną
funkcję autokorelacji natężeniowej możemy oszacować czas trwania impulsu,
który jest rzędu szerokości połówkowej funkcji 
.
Główną wadą tej metody jest to, że aby wyznaczyć czas trwania impulsu (szerokość
połówkową 
) musimy założyć
konkretną postać funkcji 
.
Najważniejsza zaleta zaś, to bardzo prosta realizacja doświadczalna pomiaru 
.
Jednakże, w wielu innych zastosowaniach,
ważna jest struktura impulsu. Jeśli pominiemy efekty kwantowe, to pełna
informacja o impulsie światła zawarta jest w funkcji opisującej pole elektryczne
fali 
:
(2)
jest obwiednią impulsu, 
oznacza centralną częstość drgań fali, a 
zależną od czasu fazę. Żeby zatem w pełni scharakteryzować impuls musimy
wyznaczyć dwie funkcje: zależną od czasu amplitudę i fazę impulsu. Wykonując
transformatę Fouriera funkcji 
możemy przejść do dziedziny częstości, w której impuls laserowy opisany
jest przez amplitudę spektralną 
oraz fazę spektralną 
. Oba
opisy: w dziedzinie czasowej i w dziedzinie częstości są w pełni równoważne
i zawierają pełną informację o impulsie. Dopiero w latach 90-tych opracowane
zostały dwie metody pozwalające na pełną charakteryzację impulsów: FROG
[3] (akronim od angielskiego wyrażenia Frequency Resolved Optical Gating)
oraz SPIDER [4] (akronim do angielskiego wyrażenia Spectral Phase Interferometry
for Direct Electric-field Reconstruction).
W najprostszej wersji metody FROG, nazywanej
“second-harmonic FROG” w doświadczeniu rejestrowany jest tzw. spektrogram 
czyli widmo drugiej harmonicznej wytwarzanej z dwóch identycznych replik
impulsu mierzonego i opóźnionych względem siebie o t
:
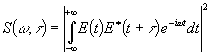(3)
przedstawiono w postaci zespolonej. Dane doświadczalne są poddawane obróbce
numerycznej, w której metodą iteracyjną odtwarzamy
czyli i .
Nie można a priori założyć, że procedura iteracyjna daje poprawne rozwiązania,
jednakże kilka lat stosowania tej metody do charakteryzacji femtosekundowych
impulsów laserowych zdaje się wskazywać, że metoda działa dobrze nawet
wtedy gdy i
mają bardzo złożone kształty. Typowy wynik stosowania metody FROG ilustruje
Rys.1, na którym pokazano amplitudę i fazę impulsu z femtosekundowego lasera
szafirowego wyznaczone w Zakładzie Optyki Instytutu Fizyki Doświadczalnej
Uniwersytetu Warszawskiego. Nie będzie przesadą stwierdzenie, że FROG jest
w tej chwili najlepiej ugruntowaną i najszerzej stosowaną metodą charakteryzacji
femtosekundowych impulsów laserowych.
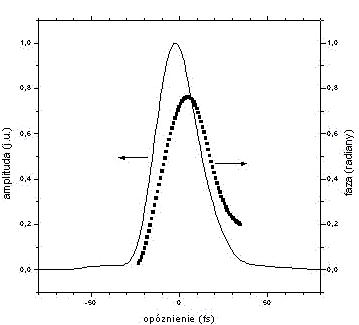
Rys.1. Amplituda i faza femtosekundowego
impulsu z lasera szafirowego. Szerokość połówkowa impulsu (mierzona dla
natężenia) wynosi ok. 20 fs. Duża zmiana fazy w czasie trwania impulsu
oznacza, że nie jest on furierowsko ograniczony – szerokość widma jest
większa niż minimalna szerokość potrzebna do wytworzenia impulsu o takim
czasie trwania.
W odróżnieniu od metody FROG metoda SPIDER
jest bardzo nowa i nie była szeroko testowana. Doświadczalnie, SPIDER polega
na rejestracji tzw. interferogramu czyli widma pochodzącego od dwóch replik
mierzonego impulsu, z których jedna jest opóźniona w czasie o 
i przesunięta w częstości o 
.
Interferogram opisany jest wyrażeniem
,
(4)
w którym
i oznaczają odpowiednio
amplitudę spektralną i fazę spektralną impulsu. Dysponując zarejestrowanym
w doświadczeniu interferogramem możemy wyznaczyć
oraz dla szeregu częstości
w widmie impulsu odległych od siebie od .
Olbrzymią zaletą metody SPIDER jest to, że amplituda i faza spektralna
są wyznaczane bezpośrednio z danych doświadczalnych bez potrzeby odwoływania
się do jakichkolwiek procedur iteracyjnych; dzięki temu unikamy potencjalnych
niejednoznaczności związanych z takimi procedurami.
III. Zastosowania
III.1. Fizyka
Mechanika kwantowa opisująca świat w mikroskali jest prawdopodobnie najlepiej przetestowaną teorią w fizyce. Jest także, co potwierdzają nie tylko laicy ale także sami fizycy, teorią zupełnie niezgodną z intuicją jaką wynosimy z życia codziennego. Dlatego też zawsze duże zainteresowanie budziły doświadczenia, w których można było zmusić obiekty kwantowe do zachowań kwazi-klasycznych. Zilustrujmy to zagadnienie na przykładzie dwuatomowej cząsteczki sodu. Załóżmy, że początkowo cząsteczka znajduje na najniższym poziomie oscylacyjnym stanu podstawowego X1S+g (Rys.2). Ruch jąder atomowych jest wtedy opisany funkcją falową tego poziomu a kwadrat tej funkcji daje prawdopodobieństwo znalezienia jąder w danej odległości od siebie. Układ jest kwantowy, a zatem skazani jesteśmy na niepewność - nigdy nie wiemy jaka jest odległość pomiędzy jądrami, a tylko jaki jest rozkład prawdopodobieństwa tej odległości. Wyobraźmy sobie, że potrafimy bardzo szybko (nieskończenie szybko?) wzbudzić cząsteczkę do stanu A1S+u. Jeśli samo wzbudzenie trwa stosownie krótko, to rozsądnym będzie założyć, że w jego trakcie odległość pomiędzy jądrami nie zmieni się. Zatem w chwilę po wzbudzeniu nasza niepewność co do odległości pomiędzy jądrami jest taka sama jak w stanie podstawowym czyli znacznie mniejsza niż dostępny w stanie A1S+ u zakres odległości międzyjądrowej R. W języku mechaniki kwantowej mówimy wtedy o wzbudzeniu spójnej superpozycji wielu poziomów oscylacyjnych w stanie A1S+u. Taką superpozycję nazwiemy pakietem falowym. W chwilę po wzbudzeniu sytuacja jest zdecydowanie niestacjonarna – jądra atomowe są bliżej siebie niż średnia odległość międzyjądrowa dla tego stanu. Wzbudzony przez nas pakiet falowy zacznie zatem “staczać się” po krzywej potencjału co odpowiada zwiększaniu odległości pomiędzy jądrami. Jednakże kiedy pakiet falowy osiągnie już położenie odpowiadające minimum energii potencjalnej jądra zdążą się rozpędzić na tyle, że “z rozpędu” pakiet falowy wespnie się na prawą część krzywej, po czy znowu zacznie staczać się w dół, itd. – będziemy obserwowali oscylacje pakietu falowego. Mamy tu zatem do czynienia z takim stanem kwantowym cząsteczki, dla którego ruch jąder bardzo przypomina klasyczny ruch dwóch mas połączonych sprężyną. Jeśli dysponujemy impulsami femtosekundowymi o stosownej długości fali, to wzbudzenie opisanego wyżej kwazi-klasycznego ruchu jąder w cząsteczce sodu nie jest żadnym problemem. Musimy jedynie oświetlić takim impulsem komórkę zawierającą cząsteczki sodu. Chcielibyśmy jednak przekonać się również czy nasza hipoteza o “dwóch kulkach na sprężynie” jest słuszna. Można to zrobić w następujący sposób. Zastanówmy się jak będzie wyglądała fluorescencja dużej liczby cząsteczek wzbudzonych femtosekundowym impulsem laserowym. W chwilę po wzbudzeniu odległość pomiędzy jądrami we wszystkich wzbudzonych cząsteczkach będzie w przybliżeniu równa Rmin. Emitowane przez te cząsteczki fotony będą zatem miały energię taka samą jak fotony impulsu laserowego. Po połowie klasycznego okresu drgań jąder odległość pomiędzy jądrami będzie w przybliżeniu równa Rmax i cząsteczki będą emitowały fotony o mniejszej energii – większej długości fali. Dokładne rachunki [5] wykonane dla tego zagadnienia dają wynik pokazany na Rys.3. Rzeczywiście widmo fluorescencji dwuatomowej cząsteczki sodu wzbudzonej femtosekundowym impulsem laserowym zależy od tego w jakim momencie czasu je obserwujemy i zmienia się cyklicznie wraz oscylacjami odległości pomiędzy jądrami. Aby taki efekt zaobserwować potrzebny jest jakiś sposób rejestracji widma świecenia naszej próbki dla różnych czasów po wzbudzeniu. Problem jedynie w tym, że okres drgań jąder w cząsteczce sodu wynosi 300 fs i mamy mało czasu na zmierzenie widma jeśli nie chcemy uśrednić go po okresie drgań. Można to zrobić w ten sposób, że fluorescencję najpierw przepuszczamy przez bramkę czasową – bardzo szybką migawkę otwieraną stosownie opóźnionym femtosekundowym impulsem laserowym a dopiero później mierzymy jej widmo. Z powodów praktycznych znacznie łatwiej jest rejestrować nie widmo fluorescencji dla danego czasu ale natężenie fluorescencji dla danej długości fali w funkcji opóźnienia pomiędzy impulsem wzbudzającym próbkę a impulsem otwierającym migawkę. Wyniki takich pomiarów [6] pokazane są na Rys. 4. Na tym samym rysunku pokazane są także wyniki kwantowo-mechanicznych obliczeń dla cząsteczki sodu. Jakkolwiek można mieć zastrzeżenia co do szczegółów, to generalnie zgodność wyników doświadczalnych z oczekiwaniami jest dobra. I tak, np. dla długości fali l =800 nm odpowiadającej odległości pomiędzy jądrami równej Rmax w doświadczeniu obserwujemy modulację natężenia z okresem odpowiadającym klasycznemu okresowi drgań jąder w cząsteczce, a pierwsze maksimum pojawia się , zgodnie z oczekiwaniami, po ok. 150 fs. Jeśli natomiast wybierzemy długość fali odpowiadającą odległości międzyjądrowej z obszaru pomiędzy Rmin i Rmax, to okres w jednym okresie drgań zauważamy dwa maksima fluorescencji – jądra dwukrotnie znajdują w tej odległości w czasie jednego okresu drgań.
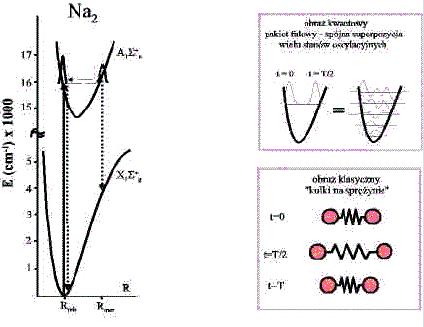
Rys.2. Ilustracja pakietów falowych w ruchu oscylacyjnym jąder cząsteczki
Na2.
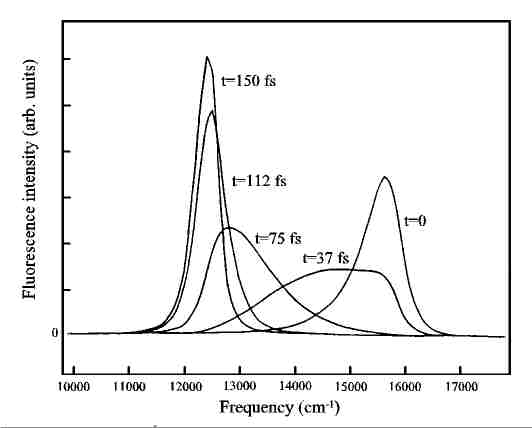
Rys.3. Obliczona fluorescencja cząsteczek Na2 wzbudzonych
impulsem laserowym (długość fali 630 nm, impuls 50 fs) mierzona w różnych
czasach po wzbudzeniu. W obliczeniach przyjęto, że bramka czasowa ma również
długość 50 fs.
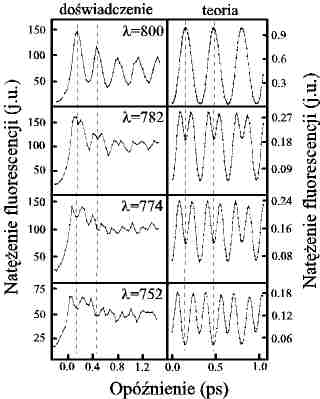
Rys.4. Zmierzone i policzone natężenie fluorescencji cząsteczek
Na2 wzbudzanych impulsem laserowym (l = 630 nm, t = 50 fs).
Przed spektrometrem umieszczono bramkę czasową otwieraną tym samym impulsem
laserowym. Opóźnienie oznacza odstęp czasu pomiędzy impulsem wzbudzającym
cząsteczki a impulsem otwierającym bramkę czasową.
III.2. Chemia
Od niepamiętnych czasów ludzie marzyli o tym, by nauczyć się wytwarzać
złoto. Jeśli nawet dziś nie do końca podzielamy motywy średniowiecznych
alchemików, to warto zauważyć, że we współczesnej nauce istnieje zagadnienie
o zbliżonej naturze i równie intrygujące jak to przed wiekami. Problem
alchemii sprowadza się, jak to już wiemy od dość dawna, do znalezienia
odpowiedniej reakcji jądrowej, w wyniku której dostaniemy jądra atomów
złota z jąder innego, łatwiej dostępnego na Ziemi pierwiastka. Jest to
w zasadzie możliwe, tyle tylko, że bardzo kosztowne i zupełnie nieuzasadnione
z ekonomicznego punktu widzenia. Jedno z największych wyzwań współczesnej
technologii polega na znalezieniu wydajnych metod wytwarzania nie pierwiastków,
a raczej związków chemicznych. Spośród różnych koncepcji w tej dziedzinie
należy wymienić, z jednej strony, biotechnologie, które wykorzystują biologiczne
“fabryki chemiczne” do wytwarzania różnych substancji z drugiej zaś inżynierię
chemiczną, w której pożądane związki chemiczne są projektowane a następnie
syntetyzowane przy użyciu różnych technik. Nie mam najmniejszych wątpliwości,
że biotechnologie mają przed sobą wspaniałe perspektywy rozwoju; już samo
poznanie i zrozumienie niezliczonych mechanizmów, które wypracowała przyroda
to wspaniała przygoda intelektualna. Jako przykład zastosowań biotechnologii
można podać np. produkcję leków nowej generacji syntetyzowanych przez rośliny
o odpowiednio zmodyfikowanym kodzie genetycznym. Niejako w cieniu biotechnologii,
która od początku stymulowana była zastosowaniami dokonuje się postęp w
innej, pokrewnej dziedzinie – i nżynierii chemicznej czyli poznaniu i kontroli
reakcji chemicznych. Trzeba tu od razu powiedzieć, że tak rozumiana inżynieria
chemiczna ma bardzo niewiele wspólnego z tradycyjną chemią. Kontrola reakcji
chemicznych jest szczególnym przypadkiem bardziej ogólnego zagadnienia
nazywanego kontrolą kwantową. Zasadniczy problem rozważany przez ludzi
zajmujących się tą dziedziną można sformułować następująco. Załóżmy, ze
mamy pewien układ kwantowy w określonym stanie początkowym (surowiec),
na który możemy oddziaływać przy pomocy fali elektromagnetycznej – impulsu
laserowego. Chcemy przeprowadzić ten układ do określonego stanu końcowego
(produkt). Pytanie brzmi: jaka powinna być postać impulsu by uzyskać największą
efektywność czyli wytworzyć możliwie dużą ilość produktu możliwie małym
nakładem energii. Tak sformułowane zagadnienie teoretyczne jest całkiem
skomplikowane. Po pierwsze musimy mieć dostatecznie dokładne informacje
o naszym układzie kwantowym, a także o jego oddziaływaniu z impulsem laserowym.
Wbrew pozorom spełnienie tego wymogu nie jest banalne – dla większości
użytecznych układów kwantowych (np. duże cząsteczki organiczne) nie mamy
szans napisania dokładnego hamiltonianu, nie wspominając już nawet o znalezieniu
poziomów energetycznych, etc. Po drugie, nawet jeśli olbrzymim wysiłkiem
uda się nam wypracować rozsądny model rozważanego układu, to sama optymalizacja
procesu jest również trudna, szczególnie jeśli oddziaływanie ze światłem
nie jest liniowe. W tej sytuacji narzuca się inne podejście do zagadnienia.
Opiera się ono na wykorzystaniu sprzężenia zwrotnego – układ doświadczalny
uczy się na “własnych błędach” . Zilustrujmy to podejście przykładem konkretnych
badań wykonanych przez grupę z Uniwersytetu w Wurzburgu w Niemczech [7].
Przedmiotem badań była cząsteczka CpFe(CO)2Cl, która po absorpcji
fotonu może rozpadać na kilka różnych sposobów (Rys.5a). Załóżmy, że chcemy
zoptymalizować wydajność jednego z kanałów rozpadu, w którym “odrywamy’
od cząsteczki jedną grupę CO oraz atom Cl. Zamiast jednak martwić się o
szczegóły budowy cząsteczki i jej oddziaływania z femtosekundowym impulsem
laserowym wkładamy trochę więcej pracy w budowę układu doświadczalnego
(Rys.5b). Informacje o wydajności wybranego kanału fotorozpadu pochodzące
ze spektrometru masowego analizującego produkty rozpadu przesyłane są do
komputera, który z kolei sprzężony jest z układem laserowym i może w dość
dowolny sposób zmieniać parametry impulsu laserowego (
i .
Do optymalizacji procesu wykorzystany został algorytm genetyczny [8]. Jego
działanie ilustruje Rys.5c. Własności impulsu laserowego zapisane są w
postaci “genu” – przedział częstości pokrywany przez widmo laserowe podzielono
na szereg odcinków i każdemu z nich przypisano określone wartości amplitudy
i fazy spektralnej. Tak skonstruowany “gen” opisuje impuls laserowy o określonych
postaciach i .
Możemy sobie wyobrazić, że jeśli losowo wybierzemy wartości amplitudy i
fazy spektralnej dla bardzo dużej liczby “genów”, to w ten sposób uzyskamy
wszystkie możliwe formy impulsu laserowego. Jednak nie wszystkie geny są
równie dobre. Niektóre z nich odpowiadają impulsom laserowym, które dają
dobrą wydajność interesującej nas reakcji rozpadu cząsteczki podczas gdy
inne nie spełniają tego warunku. Skoro już jednak zaczęliśmy naśladować
naturę, to powinniśmy być konsekwentni! Pozwólmy dobrym genom przetrwać
a złym wyginąć – informacje potrzebne do podjęcia takich decyzji mamy ze
spektrometru masowego. I to jest właściwie koniec recepty. Kłopot jedynie
w tym, że aby mieć pewność, iż znajdziemy optymalny “gen” musimy zacząć
od bardzo dużej ich populacji co nie jest rozwiązaniem bardzo praktycznym.
Znacznie prościej jest rozpocząć zabawę z niezbyt dużą populacją genów,
pozwolić im na krzyżówki, a na dodatek wprowadzić samoistne mutacje. Kiedy
wszystkie te elementy zostaną już wbudowane w program komputerowy obsługujący
doświadczenie możemy uruchomić układ doświadczalny, odchylić się w fotelu
i obserwować “walkę o przetrwanie”. Laser femtosekundowy generuje impulsy
odpowiadające poszczególnym “genom”, spektrometr masowy ocenia ich przydatność
dla wybranego kanału fotorozpadu cząsteczki a kod komputerowy decyduje
o ich przetrwaniu oraz dalszym losie (mutacje i krzyżówki). Jeśli wszystko
działa poprawnie, to w kolejnych generacjach genów pozostają tylko te,
które optymalizują wybrany przez nas kanał rozpadu. Rys.5d. pokazuje wynik
działania takiego układu. Przeprowadzono dwa doświadczenia: w pierwszym
kryterium przetrwania była optymalna produkcja Fe-Cl a w drugim CpFeCoCl
(odpowiednio białe i czarne słupki). Widać, że opisana wyżej procedura
rzeczywiście działa. Kiedy chcemy mieć dużo Fe-Cl w produktach fotorozpadu,
to układ doświadczalny sam modyfikuje impulsy laserowe tak, że wydajność
tego kanału jest duża. I możemy to osiągnąć nie wiedząc nic o budowie cząsteczki,
jej oddziaływaniu ze światłem laserowym, etc.
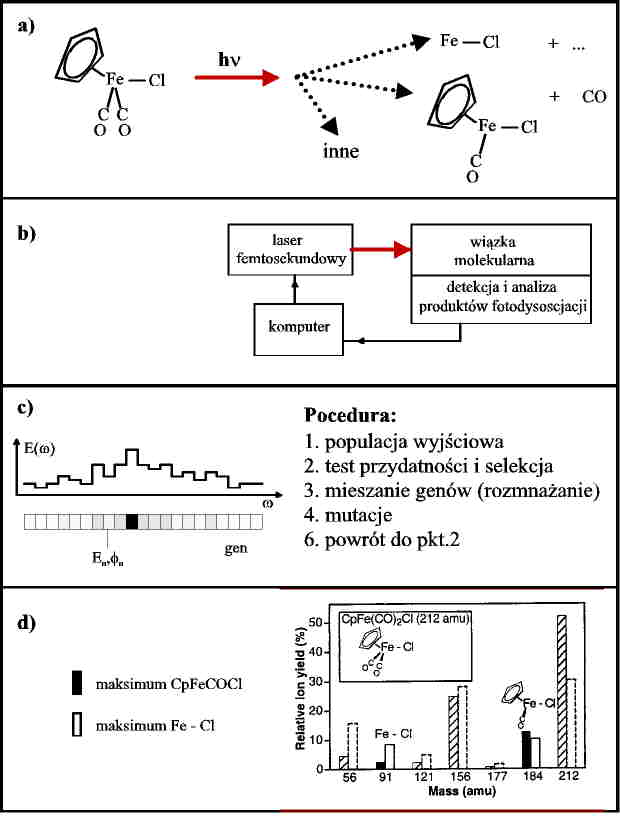
Rys.5. Budowa i wybrane kanały fotorozpadu cząsteczki CpFe(CO)2Cl
(a). Schemat blokowy układu doświadczalnego do kontroli kwantowej rozpadu
czasteczki (b). “Genetyczna” reprezentacja impulsu laserowego i opis algorytmu
genetycznego (c). Wyniki doswiadczalne (d).
III.3. Biologia
Na procesy zachodzące w żywych organizmach składa się, między innymi, olbrzymia liczba reakcji chemicznych katalizowanych odpowiednimi enzymami i zachodzących w fazie skondensowanej. Reakcje te cechuje zdumiewająco wysoka wydajność i selektywność, których ciągle nie potrafimy osiągnąć w przemysłowych procesach chemicznych. Jako przykład może tu posłużyć proces indukowanego światłem przekształcenia izomerycznego cząsteczki rodopsyny – białka występującego, między innymi, w niektórych szczepach prymitywnych bakterii. Białko to absorbuje światło i syntetyzuje cząsteczki ATP, które są podstawowym nośnikiem energii w organizmach żywych. Początkiem całego skomplikowanego procesu syntezy ATP jest przekształcenie izomeryczne chromoforu wbudowanego w cząsteczkę rodopsyny i pokazanego na Rys.6a. Chromofor, który pierwotnie jest w formie trans absorbuje foton i przechodzi do formy 13-cis. Zdumiewająca jest wydajność tego procesu – prawie 70%. Gdyby założyć, że energia wzbudzenia cząsteczki (energia pochłoniętego fotonu) rozkłada się w przybliżeniu równo na wszystkie stopnie swobody (mówimy wtedy o termalizacji energii wzbudzenia), to prawdopodobieństwo transformacji izomerycznej byłoby bliskie zeru. Ponieważ tak nie jest, to można wysunąć hipotezę zgodnie z którą, w stanie wzbudzonym formuje się pakiet falowy analogiczny do tego jaki opisałem dla cząsteczki sodu i ten pakiet “zjeżdża” po wielowymiarowej powierzchni energii potencjalnej do minimum odpowiadającego formie 13-cis. Czy można udowodnić taką hipotezę? Zrobiła to grupa naukowców z USA [9]. W doświadczeniu, przez nich wykonanym, próbka zawierająca rodopsynę oświetlana była dwoma femtosekundowymi impulsami światła. Pierwszy impuls, o długości fali dopasowanej do pasma absorpcji rodopsyny inicjował proces transformacji izomerycznej, natomiast drugi stosownie opóźniony femtosekundowy impuls o bardzo szerokim widmie służył do pomiaru widma absorpcji próbki w różnych momentach procesu transformacji. Przykładowe zmiany absorpcji próbki dla różnych opóźnień pomiędzy impulsami pokazuje Rys.6b. Analizując wyniki doświadczenia autorzy stwierdzają, że rzeczywiście hipoteza o istnieniu pakietu falowego w stanie wzbudzonym jest prawdziwa. Opisane tu badania stanowią tylko jeden z licznych przykładów zastosowania ultrakrótkich impulsów laserowych do badań procesów biologicznych. Piękno takich doświadczeń polega na tym, że pozwalają one obserwować rzeczywistą dynamikę przekazu energii w złożonych cząsteczkach, elementarne procesy tworzenia i rozpadu cząsteczek, procesy przeniesienia elektronu bądź protonu, itd.
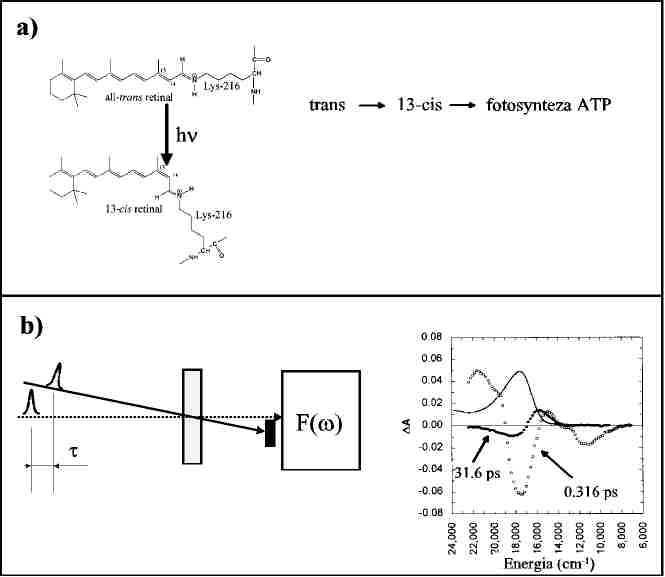
Rys.6. Wzór strukturalny chromoforu rodopsyny oraz przekształcenie
konformacyjne tego chromoforu pod wpływem absorpcji fotonu (a). Schemat
układu doświadczalnego i wyniki pomiarów (b). Krzywą ciągłą oznaczona absorpcję
próbki wtedy gdy impuls pompujacy jest zablokowany.
IV. Perspektywy
Technologia femtosekundowa jest w tej chwili dojrzałą dziedziną wiedzy. Czy osiągnęliśmy już wszystko co było do osiągnięcia? Na pewno nie. Z jednej strony, jest całkiem prawdopodobne, że w nadchodzących latach będziemy obserwowali ciągły, aczkolwiek pewnie wolniejszy niż dotychczas, postęp w generacji coraz to krótszych impulsów promieniowania. Dla wielu z nas magiczną barierą jest 1 femtosekunda poniżej której rozciąga się królestwo impulsów attosekundowych. Nie wiadomo kiedy nauczymy się wytwarzać impulsy attosekundowe, nikt jednak nie wątpi, że taka chwila nadejdzie. Drugim oczywistym kierunkiem rozwoju technik femtosekundowych jest generacja utrakrótkich impulsów w głębokim ultrafiolecie czy wręcz w obszarze promieniowania X. Gdybyśmy dysponowali takimi impulsami, to można by realnie myśleć o śledzeniu dynamiki ruchu jąder atomowych, nie przez obserwację wpływu tego ruchu na elektrony w cząsteczkach jak to robimy teraz, ale przez bezpośrednie rozpraszanie na jądrach. Wreszcie trzeci, bardzo ważny kierunek rozwoju technik femtosekundowych to wytwarzanie impulsów o coraz większym natężeniu. Historię osiągnięć w tej dziedzinie ilustruje Rys. 7. Ostatni okres burzliwego postępu trwający ostatnie 10 lat związany jest z wykorzystaniem techniki CPA (akronim angielskiej nazwy Chirped Pulse Amplification). W tej chwili w dużych układach doświadczalnych dedykowanych laserowej fuzji termojądrowej uzyskiwane są natężenia powyżej 1015 W (1 PetaWat), a w małych (zajmujących powierzchnię rzędu pojedynczych metrów kwadratowych) natężenia rzędu 1014 W. Ogniskując takie impulsy możemy dostać imponujące natężenia – aktualny rekord świata w tej kategorii to ok. 1021 W/cm2. Wydaje się, że w ramach obecnie dostępnej technologii można będzie zwiększyć tę wartość o ok. 4 rzędy wielkości czyli do poziomu 1025 W/cm2. Jednak nawet natężenia dostępne dzisiaj są wystarczająco duże by przyspieszać elektrony do prędkości relatywistycznych a także realnie myśleć o konstrukcji akceleratorów cząstek elementarnych opartych na femtosekundowych impulsach światła.
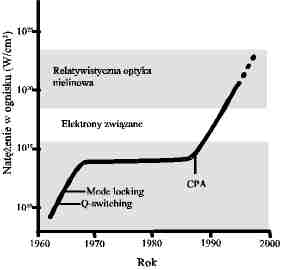
Rys.7. Historia rekordu natężenia promieniowania laserowego.
Literatura
1. C. Radzewicz, P. Wiewiór, Ultrakrótkie impulsy laserowe, Postępy Fizyki 49, 181-213, (1998).
2. D.H.Sutter et al., Opt. Lett.24, 631 (1999).
3. D.J.Kane and R.Trebino, IEEE, J. Quantum Electron. 29, 571 (1993).
4. C.Iaconis and I.A.Walmsley, IEEEE J. Quantum Electron. 35, 501 (1999).
5. P.Kowalczyk, C.Radzewicz, J.Mostowski and I.A.Walmsley, Phys.Rev.A42, 5622 (1990).
6. T.J.Dunn, J.N.Sweetser, I.A.Walmsley, and C.Radzewicz, Phys.Rev.Lett.70,3388(1993).
7. A.Assion et.al., Nature 282, 919 (1998).
8. R.S.Judson and H.Rabitz, Phys.Rev.Lett.68, 1500 (1992).
9. Feng Gai, K.C.Hasson, J.Cooper McDonald, P.A. Anfinrud, Science 279, 1886 (1998).