1. Wstęp
Natura obfituje w źródła neutrin o różnych energiach. Obok fotonów tła mikrofalowego pozostały nam z Wielkiego Wybuchu bardzo niskoenergetyczne neutrina, w ilości około 100 w każdym cm3. Niestety, nie ma na razie pomysłu na ich bezpośrednie obserwacje. Najpotężniejszymi źródłami neutrin są zapaści grawitacyjne prowadzące do supernowych. W 1987 r. zaobserwowano w 3 detektorach 24 oddziaływania neutrin przybyłych z Wielkiego Obłoku Magellana. Natomiast już od kilkudziesięciu lat rejestrowane są w wielkich podziemnych detektorach neutrina słoneczne i atmosferyczne.
Podpatrywanie słabo oddziałujących neutrin wymaga wielkich detektorów oraz chowania ich głęboko pod ziemią, aby wyeliminować tło pochodzące od promieniowania kosmicznego. Takie detektory były konstruowane już od prawie 40 lat. Pierwszy eksperyment do obserwacji neutrin słonecznych powstał na początku lat sześćdziesiątych w kopalni złota Homestake w Południowej Dakocie. Zbierana mozolnie próbka danych wskazywała, że strumień neutrin jest znacznie mniejszy niż należało się spodziewać.
Na początku lat osiemdziesiątych zbudowano dwa wielkie wodne detektory Czerenkowa do poszukiwania rozpadów protonu: IMB w kopalni soli pod Cleveland (Ohio) oraz Kamiokande w kopalni cynku w Japonii. Wprawdzie nie znaleziono rozpadów protonów, ale za to stwierdzono, że wśród neutrin atmosferycznych stanowiących tło tych poszukiwań za mało jest neutrin mionowych. Zagadka ich braku była na tyle intrygująca, że stało się możliwe zbudowanie jeszcze większej wersji wodnego detektora zwanego Super-Kamiokande przez połączone siły zespołów IMB i Kamiokande.
Do rozwiązania zagadki deficytów neutrin słonecznych i atmosferycznych od dawna proponowano hipotezę oscylacji neutrin.
2. Oscylacje neutrin
Najbardziej naturalną przyczyną oscylacji są niewielkie różnice mas cząstek. Z taką sytuacją mamy do czynienia w przypadku neutralnych mezonów K.
Jeżeli przyjmiemy, że stany masowe n1, n2 neutrin nie pokrywają się ze stanami własnymi oddziaływań słabych, to ograniczając się do 2 stanów możemy napisać:
Różnica mas powoduje, że stany n1, n2 propagują się z różną prędkością i w kolejnych punktach przestrzeni zmienia się ich wzajemna proporcja. Stąd wyprodukowany w słabym oddziaływaniu np. stan nm może w odległym punkcie oddziaływania mieć skład stanów masowych bliższy stanowi nt. Prawdopodobieństwo takiej oscylacji wynosi:
Ten prosty wzór opisuje jedynie oscylacje w próżni. W gęstej materii oddziaływania cząstek powodują dodatkowe różnice w masach efektywnych, które, jak wykazano [1], mogą doprowadzić do rezonansowego wzmocnienia oscylacji.
Oscylacje przeczą zasadzie zachowania liczby leptonowej osobno w każdej generacji, ale zasada ta została sformułowana jedynie na podstawie obserwacji i nie jest znana żadna symetria w przyrodzie, która by ją narzucała.
3. Detektor Super-Kamiokande
Super-Kamiokande schowany pod górą wysokości 1 km w kopalni Kamioka zawiera 50 tysięcy ton wody. Ma kształt cylindra o wysokości i średnicy około 40 metrów. Na ścianach umieszczono prawie 12 tysięcy fotopowielaczy, każdy o średnicy 50 cm. Rejestrują one promieniowanie Czerenkowa wysyłane przez naładowane cząstki relatywistyczne. Fotony emitowane są wzdłuż powierzchni stożka pod kątem 41o do osi wyznaczonej przez kierunek cząstek. W efekcie sygnał pojawia się w fotopowielaczach zawartych w pierścieniach o grubości proporcjonalnej do długości toru cząstki.
Detektor zbudowany przez zespół ponad stu fizyków z Japonii i Stanów Zjednoczonych pracuje bez przerwy od kwietnia 1996 roku. W jego obsłudze i analizie danych uczestniczy też Uniwersytet Warszawski.
4. Neutrina atmosferyczne
W wyniku bombardowania atmosfery przez protony i lekkie jądra pierwotnego promieniowania kosmicznego powstają kaskady hadronowe. Z rozpadów hadronów powstają neutrina o widmie energii, które w przybliżeniu opisuje zależność:
Poniżej kilku GeV są to głównie rozpady: p+ (R) m+ nm , m+ (R) e+ ne anti-nm lub p- (R) m- anti-nm , m- (R) e- anti-ne nm . Stąd neutrin (i antyneutrin) mionowych powinno być dwa razy więcej niż elektronowych. Rozbieżności w ocenach stosunku r = (nm + anti-nm)/(ne + anti-ne) są mniejsze niż 5%, podczas gdy strumień pierwotnego promieniowania kosmicznego znany jest z dokładnością gorszą niż 20%.
Do wyznaczenia stosunku r wybiera się zdarzenia z pojedynczym pierścieniem, które są zdominowane przez oddziaływania kwazielastyczne n N1 (R) l? N2 . Identyfikacja leptonu l? wyznacza zatem zapach padającego neutrina.
Średnia droga radiacyjna w wodzie wynosi około 30 cm i dlatego elektrony są źródłem kaskad elektromagnetycznych, a pierścienie przez nie wywołane są znacznie bardziej rozmyte niż pierścienie pochodzące od mionów. To rozróżnienie pozwala wyznaczyć rexp = (m- + m+)/(e- + e+) i porównać z rMC wynikającym z obliczonego stosunku strumieni neutrin r oraz ze szczegółowej symulacji eksperymentu. Wyniki przedstawia się często w postaci R =rexp/rMC. Po 2 latach zbierania danych wyznaczono R = 0,67 ? 0,006 [2].
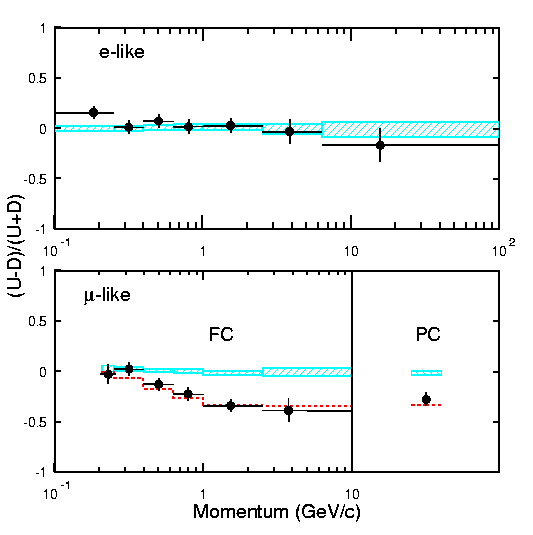
Średnia droga na oddziaływanie neutrin o energiach kilku GeV jest rzędu 108 km więc nawet pokonanie średnicy Ziemi nie powinno osłabić ich strumieni. Tymczasem w Super-Kamiokande zaobserwowano, że deficyt mionów dotyczy przede wszystkim neutrin przybywających z antypodów. Ilustruje to rys. 1 przedstawiający zależność asymetrii kątowej (U-D)/(U+D) od pędu leptonu, gdzie U oznacza strumień cząstek poruszających się do góry, a D do dołu. Histogram pokazuje zależności oczekiwane na podstawie symulacji. Widać, że podczas gdy dla elektronów wynik doświadczenia jest zgodny z oczekiwaniami, to dla mionów różnica jest bardzo znacząca.

Rys. 1
Takie zależności najlepiej wyjaśnia hipoteza oscylacji neutrin mionowych w taonowe, które przy energiach kilku GeV oddziałują znacznie rzadziej, bo mają małą szansę wyprodukowania leptonu t o masie 1,8 GeV. Krzywe zaznaczone na rys. 1 zostały otrzymane dla różnicy mas dm2 = 0,003 eV2 oraz maksymalnego mieszania [3].
5. Neutrina słoneczne
Neutrina produkowane w jądrze Słońca pochodzą głównie z następujących
reakcji:
(1) 1H + 1H (R)
2D + e+ + ne
,
(2) 7Be + e- (R)
7Li + ne ,
(3) 8B (R) 8Be*
+ e+ + ne.
Neutrina z reakcji (1) mają najniższe energie, ale jest ich najwięcej. Maksymalna energia wynosi 0,42 MeV. Reakcja (2) zachodzi znacznie rzadziej, ale wyprodukowane neutrina są monoenergetyczne, co może kiedyś umożliwić ich bezpośrednią obserwację. Ich energia wynosi 0,86 MeV. Najmniej jest neutrin z reakcji (3), ale ich energie sięgają do 14 MeV.
Dotychczas zbudowano 5 detektorów do obserwacji neutrin słonecznych. W trzech z nich ne oddziałują z jądrami 37Cl lub 71Ga. Co kilka tygodni zliczane są produkowane atomy odpowiednio 37Ar lub 71Ge. Detektory te są czułe na ne z reakcji (1) i (2).
Zupełnie inne podejście zastosowano w wodnych detektorach Czerenkowa, w których neutrina słoneczne wybijają elektrony z cząsteczek wody, przy czym elektrony zachowują kierunek neutrina. Umożliwia to wydzielenie sygnału z tła, przynajmniej dla energii neutrin powyżej 5 MeV. Jak widać na rys. 2 przedstawiającym dane uzyskane z Super-Kamiokande, po 2 latach obserwuje się wyraźny nadmiar zdarzeń skorelowanych z kierunkiem od Słońca [4].
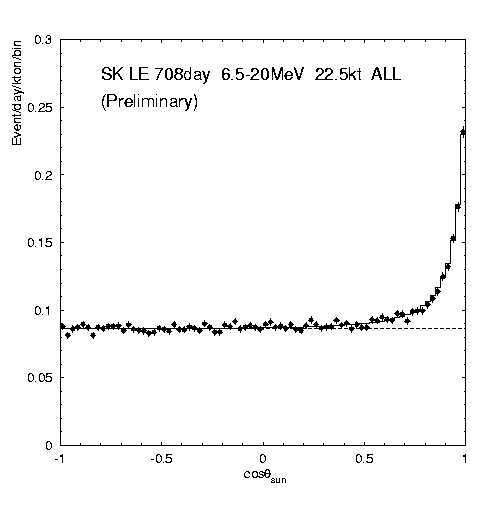
Rys. 2
We wszystkich eksperymentach zaobserwowano mniej neutrin niż przewiduje się na podstawie obliczeń teoretycznych. W Super-Kamiokande zmierzony strumień wynosi zaledwie 47,1 ? 1,5% przewidywanego.
Początkowo sądzono, że przyczyna tkwi w przybliżeniach modeli opisujących wnętrze Słońca. Jednak różnorodność danych doświadczalnych i ich dokładność pozwala na wyciąganie wniosków, które w niewielkim stopniu zależą od założeń astrofizycznych. Wyniki wszystkich eksperymentów stają się zrozumiałe, jeżeli przyjąć, że ne oscylują w nm lub nt , które przy tych energiach mogą oddziaływać jedynie z wymianą prądów neutralnych.
Możliwe są tu dwa rozwiązania: oscylacje rezonansowe wewnątrz Słońca lub w próżni w podróży ze Słońca na Ziemię. Pierwszy przypadek następuje, jeżeli dm2 jest rzędu 10-6 eV2, a drugi przy jeszcze mniejszej różnicy mas: 10-10 eV2.
Pomimo że trudno zrozumieć mierzone strumienie bez oscylacji, to jednak istnieją obawy, że możemy nie doceniać modelowych niepewności systematycznych na przykład w ocenie przekrojów czynnych w gorącej materii jądra Słońca. Dlatego dąży się do przeprowadzenia takich pomiarów, które wolne byłyby od jakichkolwiek przybliżeń modelowych.
Pierwszy taki pomiar porównuje strumienie mierzone w ciągu dnia i nocy. Jeżeli ne po drodze na Ziemię przeoscylowały w nx , to przy przejściu przez jądro Ziemi może nastąpić proces odwrotny: nx (R) ne . Przejawiałoby się to w większej liczbie zdarzeń rejestrowanych w ciągu nocy niż w ciągu dnia. Byłby to bardzo przekonujący efekt oscylacji neutrin. Niestety, na razie nie obserwuje się takiego efektu. Asymetria (N - D)/(N + D) wynosi 0,026 ? 0,021 (N to strumień w nocy, a D w dzień)[5].
Przy pewnych parametrach oscylacji widmo energii rejestrowanych neutrin powinno być wyraźnie zmodyfikowane w stosunku do typowego widma wynikającego z rozpadu 8B. Dlatego wiele uwagi poświęca się teraz w eksperymencie precyzyjnemu pomiarowi energii elektronów. Przy najwyższych energiach obserwuje się nieco mniejszy deficyt neutrin niż przy małych, ale efekt ten jest jeszcze mało znaczący statystycznie [6].
Bada się też zależność strumienia od pory roku. Niewielka modulacja tego strumienia wynika choćby ze zmiennej odległości Ziemi od Słońca. Okazuje się jednak, że większa zależność może się ujawnić na skutek oscylacji.
6. Nadzieja w akceleratorach
Jeżeli różnica mas nie jest zbyt mała, to metamorfoza neutrin może nastąpić w krótkim z konieczności czasie, jaki upływa od produkcji cząstki w akceleratorze do jej detekcji.
Pierwszy taki eksperyment o nazwie K2K zaczął właśnie zbierać dane. Jest on finansowany przez Japonię, Stany Zjednoczone i Koreę, ale uczestniczy w nim również Uniwersytet Warszawski. Neutrina produkowane są w akceleratorze KEK pod Tokio i wysyłane do dwóch detektorów: nowo zbudowanego w odległości 300 m oraz odległego o 250 km Super-Kamiokande.
Przygotowywany jest również eksperyment o nazwie Minos, w którym neutrina z Tevatronu pod Chicago będą mierzone też w dwóch detektorach, ale dalszy z nich jest budowany w odległości 730 km w kopalni Soudan w Minnesocie. Myśli się też o doświadczeniach, w których neutrina z laboratorium CERN pod Genewą byłyby rejestrowane w tunelu Gran Sasso pod Rzymem.
7. Podsumowanie
Ostatnie wyniki dotyczące neutrin atmosferycznych w Super\=Kamiokande rozpoczęły nowy, ekscytujący okres w fizyce. Obserwowane asymetrie kątowe rejestrowanych neutrin mionowych różnią się od oczekiwanych o więcej niż 5 standardowych odchyleń. Najbardziej naturalnym wytłumaczeniem tego efektu są oscylacje neutrin mionowych spowodowane maksymalnym mieszaniem się dwóch stanów o masach różniących się o około 0,05 eV.
Nieco mniej przekonujące są wyniki dotyczące neutrin słonecznych, choć trudno znaleźć dla nich inną interpretację niż oscylacje neutrin elektronowych, które z kolei sugerują mieszanie stanów o różnicach mas rzędu 10-3 eV lub 10-5 eV.
Obserwacja oscylacji świadczących o tym, że neutrina mają masę, wymaga co najmniej rozszerzenia Standardowego Modelu oddziaływań elementarnych. Informacje na temat mas neutrin są bezcenne przy konstrukcjach modeli znajdujących wspólne cechy łączące cząstki różnych generacji, a w szczególności zależności, które ułatwią zrozumienie źródła mas cząstek. Mogą one również dostarczyć klucza do odpowiedzi na pytanie, po co w naturze aż tyle cząstek, które dotychczas wydawały się nam jednakowe.
Udział Uniwersytetu Warszawskiego w Super-Kamiokande i K2K jest finansowany z grantu KBN nr 2P03B05316.