Pracownia Struktury i Dynamiki Sieci, Instytut Fizyki
Doświadczalnej, Uniwersytet Warszawski
Przeprowadzając doświadczenia numeryczne zarówno na poziomie profesjonalnym, jak i na różnych (od zaawansowanego po podstawowy) poziomach edukacyjnych, jesteśmy w stanie, z jednej strony, przewidywać nowe zjawiska fizyczne i objaśniać znane, z drugiej zaś nauczać fizyki w sposób niewerbalny, bardziej atrakcyjny. Laboratorium numeryczne [1]-[12] otwiera możliwości komplementarne w stosunku do podejść tradycyjnych - czysto teoretycznego (zwanego także analitycznym) i doświadczalnego, tym bardziej, że pozwala na to obecny poziom techniki komputerowej a także jej dostępność. W ramach laboratorium numerycznego możemy symulować i wizualizować ewolucję np. układów wielociałowych, potęgując zarówno możliwości badawcze jak i edukacyjne, zwłaszcza, że dysponujemy takim narzędziem jak Internet.
Metody Monte Carlo. Fizyka numeryczna jest stosunkowo młoda, a jej początki datują się od roku 1953, kiedy to N.Metropolis, A.Rozenbluth, M.Rozenbluth, M.Teller i E.Teller, pracujący w Los Alamos na pierwszych (odtajnionych po II wojnie światowej) komputerach, opublikowali [13] metodę Monte Carlo (opartą o proces Markowa oraz o generator liczb losowych2), która umożliwiła prowadzenie obliczeń (symulacji) numerycznych o charakterze probabilistycznym. Publikacja ta wywołała istną lawinę prac nie tylko z fizyki, czy też ogólniej mówiąc, z nauk matematyczno-przyrodniczych, ale także z innych dziedzin, w tym z ekonomii i socjologii, trwającą po dziś dzień3. Dzisiaj mówimy już nie o jednej metodzie, ale o metodach Monte Carlo zarówno klasycznych, jak i kwantowych [2, 15]. Metody Monte Carlo stanowią jeden z filarów fizyki numerycznej - drugim są metody dynamiki molekularnej.
Dynamika molekularna. Początki metod dynamiki molekularnej sięgają połowy lat pięćdziesiątych, gdy E.Fermi, J.Pasta oraz S.Ulam badali w Los Alamos, na drodze symulacji numerycznej, niecałkowalny problem anharmonicznych drgań jednowymiarowego łańcucha (składającego się z niewielkiej liczby punktowych mas połączonych ,,nieliniowymi'' sprężynkami), tzw. problem FPU [16, 17] wykazując, że np. dodanie do układu anharmonizmu nie musi prowadzić do jego ergodyczności, w przeciwieństwie do tego co wówczas powszechnie przypuszczano, a raczej do rekurencji (z okresem znacznie krótszym od przewidywanego przez znane twierdzenie Poincarego i Cermela ,,o powrotach'' [18]). Postawiło to w nowym świetle np. zagadnienie odwracalności, a także pytanie o warunki stosowalności zasady ekwipartycji energii. Obok powyższego problemu konserwatywnego, E.Fermi oraz S.Ulam zaproponowali zbadanie nieliniowego zagadnienienia dysypatywnego (zwanego czasem problemem FU [19]), w którym niewielka kulka jest podbijana (pionowo) za pomocą drgającej (np. harmonicznie) membrany, przy czym zderzenia z membraną są niesprężyste; innymi słowy, gdyby membrana nie dostarczała energii kulce, to ta traciłaby swoją energię kinetyczną bezpowrotnie. Oczywiście istnieje także konserwatywna realizacja tego problemu, gdy zderzenia kulki z membraną mają charakter sprężysty. Oba zagadnienia, badane intensywnie w poprzednich dekadach [20], dostarczyły przykładów przejścia od ruchu regularnego do chaotycznego o wielkim znaczeniu dla zrozumienia zwłaszcza tego ostatniego.
Realizowanym niezależnie przedłużeniem powyższego kierunku było odkrycie w problemie FPU (na drodze symulacji numerycznej metodą dynamiki molekularnej) przez G.Contopoulosa [21] oraz przez M.Henona i C.Heilesa [22]4konserwatywnego chaosu deterministycznego [22, 17]. Rok wcześniej dysypatywny chaos deterministyczny został odkryty (także na drodze numerycznej) przez Lorenza, który pierwszy wprowadził dziwny atraktor i tzw. ,,efekt motyla'' do fizyki, a dokładniej do fizyki atmosfery. Jak wiadomo [24], pierwszym, który wskazywał na istnienie chaosu deterministycznego był H.Poincare - to dzięki wprowadzonym przez niego powierzchniom (tzw. powierzchniom Poincarego) można z grubsza określić, gdzie go szukać i jak.
Ukoronowaniem tej fascynującej drogi badań było odkrycie w tych układach przez N.J. Zabuskiego i M.D. Kruskala w roku 1965 [25] (znowu za pomocą symulacji numerycznej) solitonów (samotnych fal), czyli przestrzennie zlokalizowanych ,,garbów'' biegnących bez zmiany swojej amplitudy i kształtu5; dwa takie solitony biegnące naprzeciw siebie zachowują się jak duchy - przenikają się wzajemnie bez zmiany kształtu, pomimo, że oddziaływanie pomiędzy elementami łańcucha ma charakter nieliniowy.
Już w drugiej połowie lat czterdziestych John von Neumann [10] wskazywał (opierając się m.in. na pierwszych wynikach uzyskanych na początku lat trzydziestych dotyczących numerycznego rozwiązywania równania Schrodingera) na możliwość rozwiązywania zagadnień niecałkowalnych w fizyce na drodze numerycznej (o ile pojawią się wystarczająco szybkie i pojemne komputery), proponując w tym celu szereg sekwencyjnych (ang. ,,step by step'') algorytmów dyskretyzujących równania ewolucji. Istotą koncepcji von Neumanna była obserwacja (sugerowana wcześniej np. przez Eulera), że sekwencyjne metody rozwiązywania zarówno równań różniczkowych zwyczajnych i cząstkowych, jak też różniczkowo-całkowych oraz różniczkowych-różnicowych są niewrażliwe na to, czy dane zagadnienie jest czy nie jest całkowalne. Stworzyło to m.in. podwaliny algorytmów, które nazywamy (deterministycznymi) automatami komórkowymi6, otwierając drogę do badania (obok wspomnianych powyżej problemów) różnego rodzaju nieliniowych zagadnień hydrodynamicznych, z turbulencją włącznie.
Drogą tą - czyli drogą badania tzw. układów złożonych, poszli B.Alder oraz T.E.Wainwright z Lawrence Livermore Laboratory, którzy odkryli korelacje długozasięgowe (tzw. ,,algebraiczny ogon'') w układzie cząsteczek odziałujących siłami molekularnymi (Lenarda-Jonesa) [26]. Autorzy ci jako pierwsi potrafili odtworzyć na drodze symulacji metodami dynamiki molekularnej przejścia fazowe gaz - ciecz oraz ciecz - ciało stałe, a także zapoczątkowali badania (oczywiście na drodze symulacji metodami dynamiki molekularnej) nad termodynamiką statystyczną stanów nierównowagowych [27]; podejście rozwinięte przez autorów i uzyskane wyniki wskazały na nowe możliwości badań, zarówno na poziomie klasycznym jak i kwantowym, nad materią skondensowaną. Wyrazem tych możliwości było otwarcie w 1959 roku nowej wielotomowej serii książkowej przez B.Aldera i współpracowników pt. ,,Methods in Computational Physics. Advances in Research and Applications''. Kontynuacją tych poczynań może być wydawana po dziś dzień przez D.Stauffera z Uniwersytetu w Kolonii analogiczna seria książkowa pt. ,,Annual Review of Computational Physics''.
Przedstawiliśmy tutaj, siłą rzeczy w ogromnym skrócie, rozwiązania wybranych zagadnień z fizyki oraz wskazaliśmy na podejścia, które wniosły nową jakość do nauk matematyczno-przyrodniczych. Zapoczątkowały one lawinę prac trwającą po dziś dzień, czego dalszym dowodem mogą być powstałe w związku z tym cenione międzynarodowe czasopisma naukowe, np. ,,Physica D. Nonlinear Phenomena'', ,,Chaos'', ,,Journal of Computational Physics'', ,,Computer Physics Communications''. Reasumując, można powiedzieć, że współczesna fizyka wspiera się na trzech filarach: fizyce doświadczalnej, teoretycznej i numerycznej. Znajduje to swój coraz szerszy wyraz także w nauczaniu fizyki.
W nauczaniu fizyka numeryczna nabrała szerszego znaczenia wraz z pojawieniem się, na początku lat osiemdziesiątych, pierwszych komputerów osobistych, jednakże na masową skalę zaznaczyła swoją obecność (wciąż w dekadzie lat osiemdziesiątych) gdy pierwsze prace z tej dziedziny pojawiły się w czasopiśmie o zasięgu światowym ,,Physics Education'', poszerzając swój zasięg wraz z powstaniem czasopisma o profilu komputerowo-edukacyjnym ,,Computers in Physics''7.
Postawmy w tym miejscu pytanie: co z tego, o czym była mowa powyżej może się przydać w nauczaniu fizyki? Aby na nie odpowiedzieć zacznijmy od obserwacji, że w istocie rzeczy stosowane algorytmy są bardzo proste - ich zasadnicze elementy sprowadzają się często do zaledwie kilku linijek, co w przypadku metod Monte Carlo jest związane jedynie z odpowiednim losowaniem liczb przypadkowych [9], a w przypadku metod dynamiki molekularnej z sekwencyjnym rozwiązywaniem równań rekurencyjnych [17], do czego komputery, maszyny z natury sekwencyjne, są sprzętowo znakomicie przystosowane. Ogólnie mówiąc, doświadczenia numeryczne opisujące np. ewolucję danego układu polegają na tym, że zadawana jest jakaś lokalna dynamika (typu probabilistycznego, deterministycznego bądź mieszana), która ma na ogół charakter elementarny, niezwykle prosty - jest to reguła mówiąca w jaki sposób układ ma się przemieszczać z danego stanu do jakiegoś wybranego sąsiedniego; dzięki temu sekwencyjnie, krok za krokiem komputer przemieszcza układ od stanu do stanu w przestrzeni fazowej. Oczywiście, powyższa ewolucja podlega dodatkowym ograniczeniom związanym z przyjętymi warunkami początkowymi lub brzegowymi, czy z ewentualnie istniejącymi w układzie zasadami zachowania lub temu podobnymi ograniczeniami fizycznymi. Ze znajomości dynamiki lokalnej nie wynika jeszcze, że potrafimy przewidzieć w sposób analityczny zachowanie układu o charakterze globalnym (integralnym) - musi nam w tym dopomóc komputer; tutaj jest właśnie miejsce na doświadczalne próbkowanie i na niepewność podobną do tej, jaka zwykle towarzyszy przeprowadzaniu realnych doświadczeń. Oczywiście w doświadczeniach numerycznych mamy do czynienia z układami małymi w porównaniu z układami makroskopowymi, o których często się wypowiadamy, dlatego należy zachować zawsze daleko idącą ostrożność, chociaż w wielu przypadkach wystarczy jako kryterium wprowadzić wymaganie, aby fluktuacje mierzonych wielkości fizycznych były znikome w porównaniu z uzyskiwanymi wartościami; ma to często miejsce nawet dla małych, rozpatrywanych tutaj układów.
Należy podkreślić, że zwłaszcza w nauczaniu ważne są nie tylko obliczenia, ale także dogodna możliwość ich wizualizacji zarówno statycznej, jak i dynamicznej - warunek ten jest spełniony obecnie z nawiązką, gdyż istnieje już wiele znakomitych i przyjaznych w użytkowaniu programów graficznych.
Postawmy teraz następne pytanie: co zrobić aby z tymi, wciąż traktowanymi jako nowe, możliwościami dotrzeć do nauczycieli i uczniów? Jak pokonać barierę psychologiczną i, mimo wszystko, merytoryczną? Odpowiedź wydaje się prosta: należy to robić poprzez numeryczne rozwiązywanie konkretnych zadań, a następnie upowszechnianie ich - jest to ważny cel, jaki stoi przed Internetem zwłaszcza w świetle realizowanego obecnie ogólnopolskiego projektu pod nazwą ,,Internet dla szkół''8.
Myślę, że konkretną wskazówką może być zamieszczony poniżej przykład dotyczący drugiej zasady termodynamiki, a dokładniej procesu wyrównywania się temperatur w wyniku przewodnictwa cieplnego poprzez ściankę diatermiczną. Proces przewodnictwa cieplnego, czy tego chcemy czy nie, jest zjawiskiem wszechobecnym - wszyscy stykamy się z nim na co dzień i zwłaszcza zimą staramy się go maksymalnie spowolnić; ubierając się ciepło zapobiegamy wychłodzeniu naszych organizmów. Jesteśmy przekonani, że zamieszczona symulacja numeryczna (przykładowo, metodą dynamiki molekularnej) dopomoże w zrozumieniu tego procesu.
Przykład ten stanowi jeden z wielu tematów przygotowywanych obecnie w Pracowni Struktury i Dynamiki Sieci Instytutu Fizyki Doświadczalnej Uniwersytetu Warszawskiego w ramach projektu pt.: ,,Termodynamika statystyczna w doświadczeniach numerycznych'' - lista tematów (poszerzana na bieżąco) oraz przykładowe symulacje zrealizowane w języku Java znajdują się pod adresem Internetowym: http://tempac.fuw.edu.pl/erka. Należy zaznaczyć, że projekt ma charakter otwarty i przystąpić do niego może każdy, kto umie programować w języku Java i przyswoił sobie elementarną wiedzę z fizyki oraz z metod numerycznych; ewentualne zgłoszenia proszę przesyłać na adres poczty elektronicznej: erka@fuw.edu.pl.
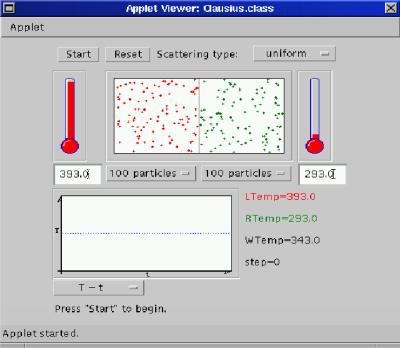
Rys. 1a: Zdjęcie migawkowe stanu początkowego układu. Liczby cząsteczek i temperatury początkowe gazu, odpowiednio w lewej i prawej części naczynia: NL=NP=100, TL=393, TP=293 |
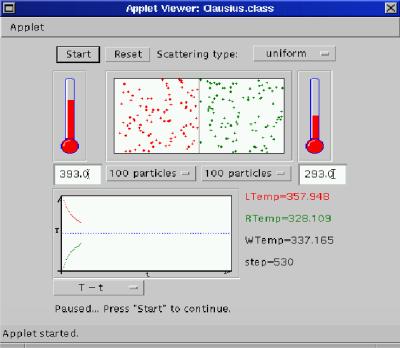
Rys. 1b: Zdjęcie migawkowe stanu układu w T=530 kroków symulacji |
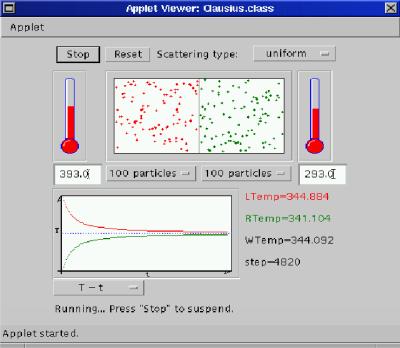
Rys. 1c: Stan układu w T=4820 kroków symulacji |
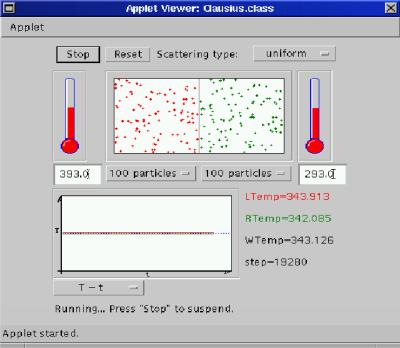
Rys. 1d: Stan układu w T=19 280 kroków symulacji |
W skrócie można powiedzieć, że największym walorem stosowania wybranych elementów fizyki numerycznej na wczesnym etapie nauczania są:
[2] Monte Carlo Methods in Statistical Physics, Topics in Current Physics, Vol.7, ed.K.Binder (Springer, Berlin 1978); Applications of Monte Carlo Methods in Statistical Physics, Topics in Current Physics, Vol.36, ed. K.Binder (Springer, Berlin 1984); The Monte Carlo Method in Condensed Matter Physics, Topics in Applied Physics, Vol.71, ed.K.Binder (Springer, Berlin 1992).
[3] R.W.Hockney, J.W.Eastwood, Computer simulation using particles, (McGraw-Hill, New York 1981).
[4] D.Potter, Metody obliczeniowe fizyki. Fizyka komputerowa, PWN, Warszawa 1982.
[5] O.G.Mouritsen, Computer Studies of Phase Transitions and Critical Phenomena, (Springer, Berlin 1984).
[6] Computer simulation of two-dimensional gas effusion, Physics Education, Vol.20, 79 (1985).
[7] L.P.Kadanoff, Computational physics: pluses and minuses, Physics Today, Vol.7, 9 (1986).
[8] S.E.Koonin, Computational Physics (Benjamin Cumm., Massechusetts 1986).
[9] R.Kutner, Metoda Monte Carlo a ruchy Browna, Delta 9, 10 (1986); R.Kutner, Mikrokomputery i co dalej?, Fizyka w Szkole 6, 333 (1986); R.Kutner, Dlaczego łatwiej o chaos niż o porządek czyli czego nas uczy prawo wzrostu entropii, Fizyka w Szkole 3, 153 (1987); W.Guzicki, R.Kutner, Egoistyczne cząstki. Symulacja komputerowa statystyki Fermiego-Diraca, Fizyka w Szkole 2, 75 (1988); R.Kutner, Symulacje komputerowe dynamiczną metodą Monte Carlo, Centrum Doskonalenia Nauczycieli, Warszawa 1989; R.Kutner, Elementy fizyki statystycznej w programach komputerowych.Cz.I. Podstawy probabilistyczne, WSiP, Warszawa, 1991; J.Ginter, R.Kutner, Komputerem w kosmos, WSiP, Warszawa 1990.
[10] K-H.A.Winkler, J.W.Chalmers, S.W.Hodson, P.R.Woodward, N.J.Zabusky, A numerical laboratory, Physics Today, Oct. 1987, p.28.
[11] R.M.Sperandeo-Mineo, G.Tripi, Microcomputer simulation of real gases. Part1. Intermolecular forces ans spatial structure, Physics Education, Vol.22, 302 (1987).
[12] R.Kutner, Symulacje komputerowe w nauczaniu fizyki ogólnej. Laboratorium numeryczne w szkole, Materiały IV Krajowej Konferencji ,,Informatyka w Szkole'', str 83, Wałbrzych 1988.
[13] N.Metropolis, A.Rozenbluth, M.Rozenbluth, M.Teller, E.Teller, Equation of state calculations by fast computing machines, J.Chem.Phys., 21, 1087 (1953).
[14] R.Zieliński, Generatory liczb pseudolosowych. Programowanie i testowanie na maszynach cyfrowych, WNT, Warszawa 1972.
[15] Quantum Monte Carlo Methods in Equilibrium and Nonequilibrium Systems, ed. M.Suzuki, (Springer, Berlin 1987).
[16] E.Fermi, J.R.Pasta, S.M.Ulam, Studies of Nonlinear Problems, Los Alamos Scient. Lab., Rep, LA-1940 (1955); Collected Works of Enrico Fermi, Vol.II, p.978, Univ. of Chicago Press, 1965; J.L.Tuck, M.T.Menzel, Superperiod of the Nonlinear Weighted String (FPU) Problem, Adv. in Mathem., 9, 399 (1972).
[17] R.Kutner, Elementy mechaniki numerycznej, WSiP, Warszawa 1990.
[18] J.P.Terlecki, Fizyka statystyczna, PWN, Warszawa 1968.
[19] G.M.Zaslavskij, Statistical Irreversability in Nonlinear Systems, (Nauka, Moscow 1970); A.J.Lichtenberg, M.A.Lieberman, Regular and Stochastic Motion, Chap.3, (Springer, Berlin 1983).
[20] P.Pierański, Jumping particle model. Period doubling cascade in an experimental system, J.Physique 44, 573 (1983); P.Pierański, P.Małecki, Noisy precursors and resonant properties of the period-doubling modes in a nonlinear dynamical system, Phys.Rev., A 34, 582 (1986); Z.J.Kowalik, M.Franaszek, P.Pierański, Self-reanimating chaos in the bouncing-ball system, Phys. Rev., A 37, 4016 (1988).
[21] G.Contopoulos, On the Existence of a Third Integral of the Motion.
[22] M.Henon, C.Heiles, The Applicability of the Third Integral of Motion: Some Numerical Experiments, Astr. J., 63, 1 (1963).
[23] G.H.Lunsford, J.Ford, On the Stability of Periodic Orbits for Nonlinear Oscillator Systems in Regions Exhibiting Stochastic Behavior, J.Math.Phys., Vol.13, 700 (1972).
[24] J.P.Crutchfield, J.D.Farmer, N.H.Packard, R.S.Show, Chaos, Scient. Am., Dec. 1986, 38; C.Grebogi, E.Ott, J.A.Yorke, Chaos, Strange Attractors, and Fractal Basin Boundaries in Nonlinear Dynamics, Science, Vol.238, 585 (1987);
[25] N.J.Zabusky, M.D.Kruskal, Interaction of ,,Solitons'' in a Colisionless Plasma and the Recurrence of Initial States, Phys.Rev.Lett., 15, 240 (1965); M.Toda, Theory of Nonlinear Lattices, Springer Series in Solid-State-Sciences, Vol.20, (Springer, Berlin 1981); A.Sym, Solitony, Postępy Fizyki, Tom 31, 3 (1980).
[26] B.J.Alder, T.E.Waiwright, Studies in molecular dynamics I: general method, J.Chem.Phys., 31, 459 (1959); B.J.Alder, T.E.Waiwright, Studies in molecular dynamics II: behaviour of a small number of elastic spheres, J.Chem.Phys., 33, 1439 (1960).
[27] B.J.Alder, T.E.Waiwright, Phase transitions in elastic disks,
Phys. Rev., 127 (2), 359 (1962).
2 Dokładniej rzecz biorąc generator taki, czyli na ogół rekurencyjna reguła matematyczna, produkuje liczby pseudolosowe [14].
3 Spektakularnym, a jednocześnie prostym przykładem ilustrującym działanie metody Monte Carlo jest symulacja numeryczna ruchów Browna - jeden z autorów niniejszej pracy (RK) miał okazję mówić już o tym [9].
4 Dokładniej rzecz biorąc, autorzy ci badali zagadnienie astrofizyczne ruchu gwiazdy w galaktyce mającej symetrię walcową - dopiero G.H.Lunsford i J.Ford [23, 17] pokazali w roku 1973, że zagadnienie to jest równoważne po prostu zagadnieniu drgań układu trzech sprzężonych anharmonicznych oscylatorów.
5 Soliton (w dosłownym tłumaczeniu samotnik) został zaobserwowany na jednym z kanałów w Szkocji przez J.Scott-Russella - dwustronicową pracę na ten temat opublikował On w materiałach Królewskiego Towarzystwa w Edynburgu w roku 1844.
6 Istnieją także analogiczne automaty probabilistyczne oraz hybrydowe.
7 Obecnie czasopismo to nosi szerszą nazwę ,,Computing in Science and Engineering'' (a jego wydawcą jest American Institute of Physics) i ma znacznie szerszy charakter.
8 Analogiczne projekty realizowane są właśnie w wielu krajach zachodnich w tym w Stanach Zjednoczonych.
9 Pod pojęciem ,,neutralnej ścianki diatermicznej'' rozumiemy ściankę, której temperatura Tw nie zaburza procesu wymiany energii - łatwo sprawdzić, że wtedy należy przyjąć Tw=NLTL/N+NPTP/N.
10 Rysunki 1a-1d stanowią po prostu zdjęcia migawkowe apletu wykonane w czterech chwilach i pokazują kolejne stadia ewolucji układu - opisy wykonano po angielsku, aby utrzymać jednorodność języka (gdyż standardowe informacje Javy udzielane są w tym właśnie języku; może warto rozszerzyć Javę tak, aby w zależności od potrzeb funkcjonowała w wybranym języku narodowym.
11 Co więcej, istnieją nawet gotowe systemy
znacznie ułatwiające pokonanie i tej przeszkody, np. Mathematica lub Mapple.