Badanie współczynnika tarcia dynamicznego i statycznego obiektu na równi pochyłej.

Przyrządy pomiarowe (układ Pasco):

  • równia pochyła o zmiennym kącie nachylenia
  • sonda położenia (ultradźwiękowa)
  • wózek o różnej masie M (=0.49 +/- 0.05 kg), 2M i 3M
  • program komputerowy Science Workshop

    • Pomiar tarcia dynamicznego.

        W eksperymencie badano przyspieszenie wózka o różnych masach (M,2M,3M) za pomocą sondy położenia, dla dowolnych kątów nachylenia równi. W przypadku tarcia poślizgowego unieruchomiono jedno i dwa kółka wózka. Schemat eksperymentu obrazują rysunki (1,2). Program komputerowy umożliwiał wykonanie pomiarów zależności położenia, prędkości i przyspieszenia od czasu. Do opisu przyspieszeń w obu przypadkach skorzystano z równań ruchu:

    M a1=M g sin(alpha)+ Fo (wjeżdżanie) oraz M a2=M g sin(alpha) – Fo (zjeżdżanie), gdzie:

    a1,a2 – przyspieszenia,
    g – przyspieszenie ziemskie,
    alpha– kat nachylenia równi,
    Fo - siła oporu.
     Z eksperymentu możemy wyznaczyć przyspieszenia a1 i a2 co pozwala na określenie Fo ze wzoru:
    Fo =M  (a1-a2)/2.
    przy założeniu
    Fo=mi M g cos(alpha), (gdzie mi - współczynnik tarcia)
    wyznaczamy
    mi=(a1-a2)/(2 g cos(alpha)).
    Przeprowadzono kilka serii pomiarowych dla obu przypadków tarcia. Otrzymano następujące wyniki:
     
    a1 (m/s2) a2 (m/s2) Fo (N) mi
    M 0.74 0.65 0.022 0.0047
    2M  0.75 0.66 0.043 0.0047
    3M 0.76 0.67 0.067 0.0047
    Tabela 1. Tarcie toczne , alpha=10o
     
    a1(m/s2) a2 (m/s2) Fo(N) mi
    M 3.27 0.42 0.71 0.15
    2M 3.25 0.37 1.38 0.15
    3M 3.21 0.32 2.07 0.15
    Tabela 2. Tarcie poślizgowe , a=16o

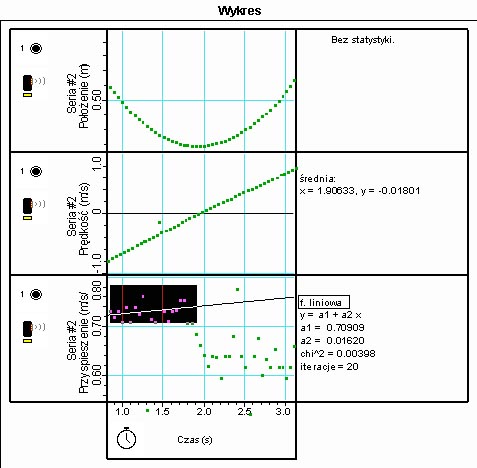
    Poniżej znajduje się przykładowy zestaw wykresów obrazujący położenie, prędkość i przyspieszenie wózka na równi pochyłej. Na podstawie wykresu ( a(t) , gdzie t – czas ruchu), można wywnioskować, że wartość opóźnienia jest większa w pierwszej fazie ruchu, na skutek działania siły tarcia oraz składowej siły ciężkości. W drugiej fazie ruchu następuje spadek przyspieszenia z analogicznych powodów. Różnice te są jednak nieznaczne, czego można się spodziewać biorąc pod uwagę stopień precyzji doświadczenia.

    Wykres 1. Tarcie poślizgowe

        Na podstawie otrzymanych wyników pomiarowych można uznać, że współczynnik tarcia jest stały i w tego typu doświadczeniach nie zależy od prędkości.

    Wykres 2. Tarcie toczne

    Rysunek 1. a) pierwsza faza ruchu b) druga faza ruchu oraz tarcie statyczne
     

    Pomiar tarcia statycznego.

        Zbadano również tarcie statyczne dla klocka drewnianego o masie (M=0.11ą 0.05 kg) na którym dodatkowo naklejona była powierzchnia z materiału. W tym przypadku skorzystano ze wzoru:
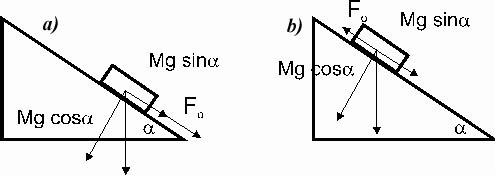
    Ft=M*g*sina,
    gdzie Ft – siła tarcia statycznego. Zwiększano kąt nachylenia równi aż do momentu zaobserwowania ruchu klocka. Wyliczono siłę dla obu powierzchni trących. Wyniki wpisano do poniższej tabeli:
     
     
    powierzchnia kąt a nachylenia równi Ft(N)
    z drewna 10o 5.87
    z materiału 11o 10.79
    Tabela 3. Tarcie statyczne
        Schemat doświadczenia dobrze obrazuje rysunek 2. Zgodnie z przewidywaniami siła tarcia statycznego jest dużo większa niż siły tarcia tocznego i poślizgowego (tabele 1 i 2).