Pomiar wymiany energii wahadeł sprzężonych za pomocą komputera.

    Układ pomiarowy wykorzystany w naszym doświadczeniu zbudowany jest z dwóch fotokomórek i identycznych, drgających między nimi wahadeł umieszczonych na jednej wspólnej nici dzięki której przekazywana jest energia. Fotokomórki połączone są do komputera poprzez konsolę pomiarową obsługującą dyskretne wyjście/wejście której budowa oparta jest na porcie równoległym (LPT) komputera klasy IBM PC. Kulki które pełnią rolę masy w  wahadle są  umieszczona w ten sposób, że w stanie spoczynku przerywają tor świelny odpowiadającej jej fotokomórki.
git
 

Nasz pomiar bazuje na wyznaczeniu zmian energii obu wahadeł. Wiadomo że w momencie zerowego wychylenia wahadła jego enrgia całkowita jest równa energii kinetycznej E=E_k gdzie Ek opisujemy następująco:

(1)     E_k=(mv2)/2

gdzie m jest masą drgającego wahadła, a v jego prędkością w danym momencie. Wiedząc, że

(2)  v=s/t

przekszałcamy wzór 1 do postaci:

(3)  E_k=(ms2)/(2t2)

gdzie s jest średnicą kulki wahadła, a t czasem  przelotu tej kulki przez bramkę świetlną. Obliczona energia przedstawiona jest na wykresach zależności E(t).
     Pomiar komputerowy bazuje na wykorzystaniu wzoru 3. Mając dane masę i średnice kulek obu wahadeł pomiar nasz ogranicza się do pomiaru czasu jaki upływa od momentu wejścia kulki w światło fotokomórki do momentu wyjścia.
 Program użyty w doświadczeniu pracuje w systemie DOS co pozwala wykorzystać zegar systemowy do zapisania  czasu przy każdym „wejściu” i „wyjściu” kulki z fotokomórki. Następnie dane te są od siebie odejmowane, co daje nam czas przelotu kulki przej bramkę z dokładnością do jednej setnej sekundy. Otrzymane w ten sposób dane są podstawiane do wzoru 3. Po odpowiednim przeskalowaniu i podstawieniu wartości wyniku do procedur graficznych możemy oglądać zmianę enrgii wahadła na ekranie monitora. Aby ułatwić obserwatorowi doświadczenia śledzenie zależności energii obu wahadeł na ekranie wyświetlono „gridy”, dzięki czemu doskonale widać, że kiedy energia kinetyczna jednego wahadła jest równa zero, E_k  drugiego osiąga lokalne maximum.
     Pomiar wykonywany jest w warunkach rzeczywistych, więc na wahadła działa siła tarcia związana z oporem powietrza, która jest wprost proporcjonalna do prędkości wahadeł, więc energia drgań maleje wykładniczo.
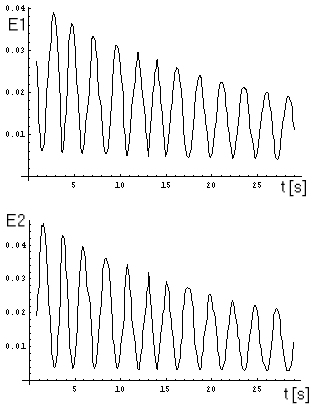
    Korzystając z wartości energii odczytanych z przykładowego pomiaru za pomocą programu Mathematica3.0 otrzymaliśmy wykresy energii dla każdego z wahadeł.

E(t)=A + B e-Ct cos2(D+Ft)

gdzie:
    A=0.004, B=0.04, C=0.035, D=56, F=1.37.
 

Program: wahsprze.exe
Źródło: wahsprze.cpp