
Falę stojącą możemy potraktować jako wynik interferencji dwóch fal biegnących z przeciwnymi zwrotami (F1(x,t) i (F2(x,t)). Możemy to wykazać poprzez zsumowanie fali F(x,t) , danej wzorem
(1) F1 (x,t)=A sin (2Pi(x/lambda - t/T))i fali F(x,t), danej wzorem
(2) F2 (x,t)=A sinI(2Pi(x/lambda + t/T)).Wykorzystamy przy tym związek
sin(alpha) + sin(beta) = 2 sin[(alpha + beta)/2] cos [(alpha - beta)/2]Dodając wzór 1 do wzoru 2 dostajemy:
(3) F(x,t) = A sin(2Pi(x/lambda - t/T)) + A sin(2Pi(x/lambda + t/T)) =Wielkości lambda i T, występujące we wzorze 3 są tymi samymi wielkościami, które występują we wzorach 1 i 2. A więc związek pomiędzy lambda i v dla fal biegnących i fal stojących musi być taki sam.
= 2A sin(2Pix/lambda ) cos(2Pit/T).
(4) v=f*lambdamożemy w bardzo prosty sposób wyliczyć prędkość rozchodzenia się fali dźwiękowej w powietrzu.

Za pomocą programu Cool Edit Pro możemy przy użyciu mikrofonu odczytać wartość chwilowego natężenia dźwięku. Przy pomocy programu FX generujemy falę o znanej częstotliwości. Najmniejsze natężenie dźwięku występuje w węźle fali stojącej. Przesuwając mikrofon między dwoma naprzeciw siebie ustawionymi źródłami fali akustycznej (głośnikami) o częstotliwości f odnajdujemy odległość między dwoma kolejnymi węzłami. Odległość ta jest połówką długości fali. Podstawiając wartość lambda i f do wzoru 4 otrzymujemy wartość prędkości dźwięku.
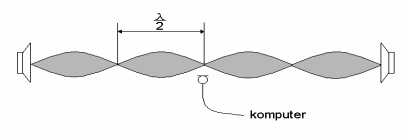
Vśr = 321,6 m/s
Programy użyte w dowiadczeniu można odnaleźć w internecie pod adresami :
Cool Edit Pro - ftp://ftp.syntrillium.com/pub/cep/cep11dmo.exeKorzystano z książki Jerzego Gintera "FIZYKA III".
FX - ftp://ftp.fh-wiesbaden.de/pub/win/win95/sounds/fx15.zip