Dyfrakcja światła na szczelinie

Zagadnienia Układ pomiarowyPrzeprowadzenie pomiarów Opracowanie wyników

Zagadnienia

Układ pomiarowy


Zdjęcie układu pomiarowego.


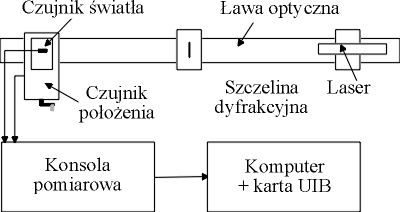
Schemat układu pomiarowego do badania dyfrakcji światła na szczelinie

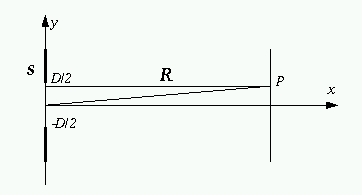
    Układ pomiarowy zbudowany jest na  ławie optycznej. Źródłem światła jest laser półprzewodnikowy o długości światła lambda  = 632 nm.  Czujnik światła w postaci fototranzystora jest umieszczony w obudowie gdzie światło doprowadza się światłowodem zaś jego drugi koniec zamocowany jest w precyzyjnym przesuwie. Położenie czujnika w osi prostopadłej do rozchodzenia się światła mierzymy czujnikiem zintegrowanym w układzie precyzyjnego przesuwu. Szczelinę umieszczamy w odległości ok 1 m od czujnika światła (dlaczego ??).  Geometria układu przedstawwiona jest na poniższym rysunku.


Geometria układu:  s- szczelina dyfrakcyjna, P -płaszczyzna obrazu, R - odległość między szczeliną a płaszczyzną obrazu, D - szerokość szczeliny

Przeprowadzenie pomiarów

    Pomiary przeprowadzamy przy pomocy programu "dyfrakcja_na_szczelinie.vi".  Program ten uwzględnia kalibrację czujnika położenia. Przed rozpoczęciem pomiaru ustawiamy parametry pomiaru:     Następnie ustawiamy przesów w skrajnym zerowym położeniu oraz uruchamiamy program.  Położenie czujnika zmieniamy kręcąc korbką przesuwu. Należy uważać by nie przekraczać skrajnych dopuszczalnych położeń by uniknąć zniszczenia czujnika kąta (wyczuwalny opór !!!!). W czasie wykonywania pomiaru powinno unikać się wprowadzania drgań stołu ze względu na małą stabilność elementów na ławie optycznej. Program przerywa pracę automatycznie w momencie przejścia czujnika w drugie skrajne położenie. Po zakończonym pomiarze zapisujemy dane na dysk w celu analizy.


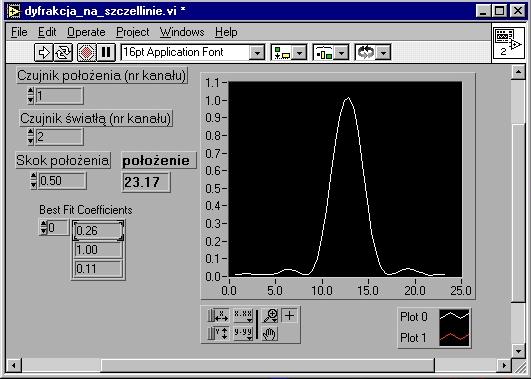
Zrzut ekranu programu do pomiaru dyfrakcji światła. Widać wynik przeprowadzonego pomiaru.

Opracowanie wyników

    Analizę otrzymanego wyniku przeprowadzamy pod kątem wyznaczenia rozmiaru szczeliny na której uginało się światło.  W tym celu musimy dopasować dane eksperymentalne do teoretycznej  zależności opisującej rozkład natężenia światła w przypadku ugięcia na pojedyńczej szczelinie:
gdzie 
gdzie dla małych kątów możemy powyższe wyrażenie zapisać w postaci (patrz geometria układu):
Ułatwieniem na drodze dopasowania jest przeskalowanie danych  pomiarowych. Otrzymane z pomiaru natężenie należy unormować do jedynki, a wartości na osi y  przeskalować tak by dla otrzymanego maksimum odpowiadało y = 0, a wartości przesunięcia zamienić na odpowiednie wartości kąta ugięcia.  Poniższy wykres przedstawia punkty otrzymane na drodze pomiaru oraz wykres zależności do nich dopasowanej (rozmiar szczeliny b = 0.13 mm)


Wynik dopasowania danych pomiarowych zależnością teoretyczną. Wynik dla szczeliny 0.13 mm skalowany w parametrze Beta.

Podstawy  programu w jezyku Mathematica. (nie całość !!!) Wygodne jest używanie polecenia Table do przekształcania danych. Pomoc do dowolnego polecenia to np: ??Plot. 
lista1 = ReadList["dane-szczelina_01.dat", {Number, Number}]; (*odczyt danych z dysku*)
ListPlot[lista1, PlotStyle -> PointSize[0.02], AxesLabel -> {"x [mm]", "I [V]"}] ; (*rysowanie wykresu*)
Plot[funkcja[parametr],{zakres zmian parameteru}]
(* dodatkowe definicje*)
lamb = 632 10^-9;  (*Dlugosc swiatla laserowego He - Ne*)
k = 2 Pi/ll; (*Wektor falowy*)
<< Statistics`NonlinearFit`  (*ściągamy pakiet do nieliniowego dopasowywania*)
NonlinearFit[dane, postać_funkcji, x, {lista_parametrów}]











Sprawozdanie  powinno zawierać:






Literatura