Now we analyze magnetization process in a film with the stripe domain structure (DS) neglecting the domain wall width, see Fig.2. The total volume energy density of DS is the sum of the domain wall, Zeeman and demagnetizing energies:
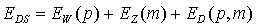 |
(1.8) |
For periodical stripe domains with domain size D (means size of a domain magnetized opposite the applied field) the two first terms in Eq.8 can be easily obtained from a geometrical consideration. So, Eq.8 now becomes
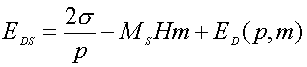 |
(1.9) |
with m= (D+-D–)/p. The demagnetizing energy is a rather complicated function and it can be represented as a series of its parameters (see the third term in Eq. A1, see the Appendix). The energy (Eq. 1.9) has two independent parameters describing domain geometry (e.g. m and p or D+ and D–) which can be used for EDS minimization. We choose m and p. So, the equilibrium normalized magnetization and DS period are defined by the two equations:
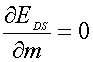 |
(1.10) |
and
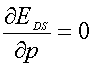 |
(1.11) |
The explicit shape of Eqs. (1.10) and (1.11) one can find in the Appendix. Here we discuss the numerical solution of the system of equations (1.10) and (1.11). They are plotted in Fig. 1.3-1.5. In Figs. 1.3 and 4 we plot the film magnetization and inverse reduced domain period (p/d) vs H/4 π MS for different values of the ratio between the characteristic length and film thickness.
Using Eqs. 1.10,.11 one can obtain the useful, for experiment analysis, description of: (i) domain period p0 for H/4π M S <<1 and (ii) the initial susceptibility χ (=dM/dH H→0). In zero-field case the domain period is determined by the magnetostatic and domain wall energies competition and the equilibrium p0 can be easily calculated from the equation (see the Appendix):
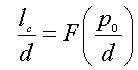 |
(1.12) |
where F(p0/d) is the function defined in the Appendix and plotted Fig. 1.5.
Knowing the material film parameters lc and d one can calculate the zero-field domain period with the help of the plot shown in Fig. 1.5, and contra versa. Solving numerically Eq.12 we find the equilibrium domain period as a function of the film thickness, see Fig. 1.6. It is important to note that the equilibrium domain period reaches its minimum at the certain film thickness which real meaning depends on the characteristic length of material. In the limiting case – large film thickness – the domain period grows proportionally to d1/2 as it is predicted by the above simplified theory (see Eg. 1.3). The Fig. 1.6 allows us compare the results obtained by rigorous calculations (Eq. 1.12) and the simple model (Eq. 1.3).
The initial magnetic susceptibility is given by χ = dM/dH =(1/4 π ) dm/dh and can be found by differentiating of Eq.(A1) with respect to h
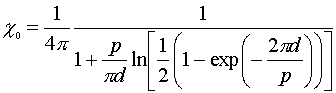 |
(1.13) |
Thus, Eq. 1.13 gives the initial susceptibility of stripe domain structure as a function of domain period (see Fig. 1.7). Passing in Eq.(1.13) to the limit p0→0 (which is a case of smallest domain wall energy and a dense domain structure, e.g. because of low anisotropy constant) one can arrive at χ0=1/4 π. The same result was previously obtained from Eq. 1.6 on the basis a simplified model. In the opposite limit, when p→∞ (or p>>d) Eg. 1.13 gives that χ→∞. Indeed, as it seen from Fig. 1.3 the susceptibility becomes infinity large before the saturation (the jumps on the m(H)-curves). Obviously, after saturation χ=0. Notice, the right side of Eq. 1.13 only includes geometrical parameters of the film and domain structure: d and p. In general, the magnetic susceptibility is affected by many factors, e.g. coercivity. The last may be a reason for a difference between values of χ measured from the virgin magnetization curve (or magnetization hysteresis loop) and determined from a DS image. Calculations of χ from analysis of domain structure images is more easy with the help of another option our experiment – registration of magnetic hysteresis loop .
One can use these figures to determine the characteristic length and the domain wall energy of a given film. Indeed, using these plots (Figs. 1.3 -1.6) and utilizing the measured domain period and domain sizes at different values of the magnetic filed it easy to determine with the help of the above given theory the material parameters: MS and χ
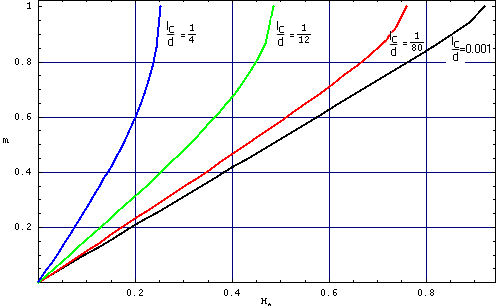 |
| Fig. 1.3 Film magnetization (m) as a function of the normalized field (h=H /4 π MS) calculated from Eqs. A2 and A3 for different values of lc/d. Note, the curve representing the case lc/d=0 is also well described by the simplified model, see Eq. ~1.6. |
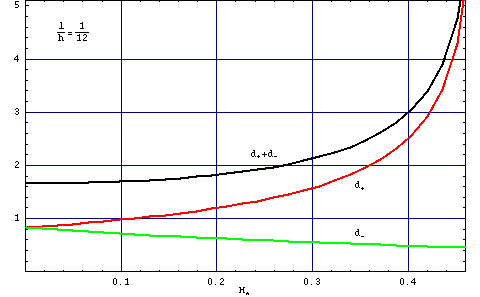 |
| Fig. 1.4 Normalized domain period (p/d) as a function of the normalized field (h) for lc/d=1/12. |
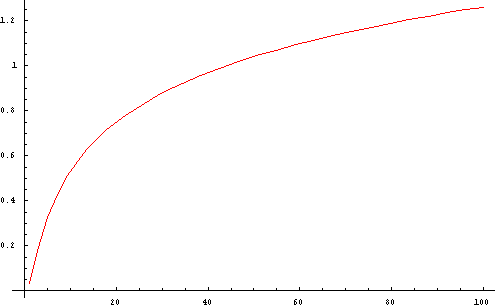 |
| Fig 1.5 Function F(p/d) used in Eq. 1.12. |
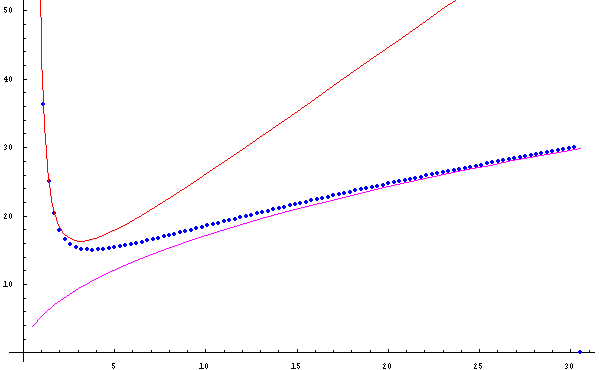 |
| Fig. 1.6. Normalized domain period (p/lc) as a function of the normalized film thickness (d/lc) for H=0. The red curve – is calculation with the Kaplan-Gehring model (Eq. 1.14), the blue one – Kooy-Enz theory (Eqs. A2 and A3), and the magenta curve is the simple dependence given by Eq. 1.3. |
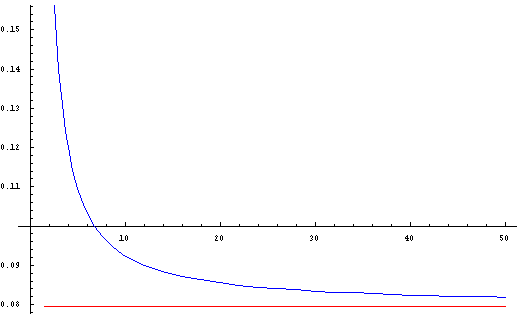 |
| Fig. 1.7. Initial magnetic susceptibility as a function of the inverse domain period, z=2 π d/p. The red line shows χ=1/4 π. |
Domain structures of ultrathin films.
The physics of domains in bulk materials and micron-sized films seem to be well understood. But domain patterns of ultrathin films exhibit many new features: unusually sharp thickness dependence of domain sizes and strong reconstruction of magnetization distribution in domains related to changes of magnetic anisotropy which are of great interest and essential for an understanding of fundamental physics. Now we apply the Koy-Enz theory for analysis of the thickness dependence of the domain period in a wide scale of thickness changes at H=0. Solving numerically Eqs.A5 and A6 we find the equilibrium domain period as a function of the film thickness, see Fig.6. In the ultrahin regime when d < lex (lex=(A/(2 π MS2))1/2, where is the exchange length and A is the exchange constant) the domain period drastically increases as the film thickness decreases. This is the case of ultrathin magnetic films (d is only a few monoatomic layers) and now such films are object of intensive studies. In the ultrathin limit the thickness dependence of the zero-field DS period can be well approximated by a simple formula (Kaplan and Gehring, 1993):
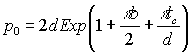 |
(1.14) |
where b= -0.666. In the opposite limiting case- large film thickness – the domain period grows proportionally to d1/2 as it is predicted by the above simplified theory (see Eg. 1.3).
To summarize, in Fig.6 we plot the thickness dependencies of the zero-field equilibrium domain period calculated in the frameworks of the three models: i) the rigorous Kooy and Enz model which is valid in the full scale of the thickness changes; ii) Kaplan and Gehring model (Eq. 1.13) which validity is restricted by the ultrathin regime, d <lc and iii) a simple model (Eq. 1.3) which well describe p(d)-dependence for thicker films. As it seen from Fig. 1.6 in the ultrathin regime the domain periods could be significantly large. In general, one can expect ultrathin film in a practically monodomain state – large magnetic domains with geometry determined mainly by coercivity rather than magnetostatic forces. However, domain size drastically decreases down to a sub-micrometer scale while approaching the thickness at which the characteristic length falls practically to zero, e.g., because of decreasing the anisotropy constant.
Appendix.
The energy of a stripe domain structure is given by the Kooy and Enz model (1960):
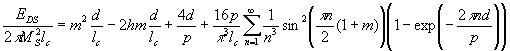 |
(A1) |
where m=<M>/M S and h=H/4pMS is the normalized field applied perpendicular to the film plane. There are two parameters which may minimize the DS energy (Eq.A1): e.g., domain period (p) and the normalized magnetization (m). The equilibrium domain structure parameters can be found by minimization of energy (A1) with respect to m=M/MS and p, accordingly:
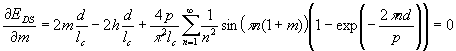 |
(A2) |
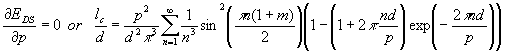 |
(A3) |
Solving Eqs. (A2) and (A3) one can calculate the equilibrium film magnetization, domain sizes and domain period as functions of the applied magnetic field. Equations A2 and A3 could be simplified if h=0 (the zero-field case). It follows from Eq.A2 that since h=0, the film magnetization m=0. By inserting the last into Eq. A3 one can arrive at
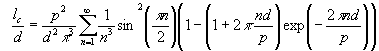 |
(A4) |
or
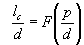 |
( A5) |
where
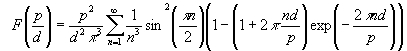 |
( A6) |
References:
- C. Kittel Phys. Rev. 70 (1946) 965.
- C. Kooy and U. Enz, Phillps. Res. Repts. 15, 7 (1960).
- B. Kaplan and G.A. Gehring, J. Magn. Magn. Mater. 128, 111 (1993).
- A. Hubert and R. Schäfer, Magnetic Domains., Springer, Berlin (1998).