Now we know that magnetic domains appear to minimize the total system energy. Indeed, as usually any system try to reach the state in which its total energy becomes minimal one. The domain appearence minimizes the total energy of the sample by a lowering of the demoganetizing energy.
Let us consider the total energy of a stripe domain structure (see Fig. 1.2) of uniaxial ferromagnetic film which is infinite in lateral directions (i.e. lateral sizes Lx and Ly are much larger than d ) . In zero-field case the domains structure consists of “up” and “down”– magnetized domains and its the total energy has two contributions: the domain wall energy, Ew (which includes the anisotropy and exchange energies) and so-called magnetostatic energy, Ed:
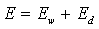 |
(1.1) |
The energy related with domain walls is Ew=σS N, where σ is the surface energy density of a domain wall, N=2 Lx/p is the number of domain walls in the film, S=Lyd is the area of one wall, and p is the domain period, see Fig. 1.2. So, from the above formula one can easy obtain Ew=2 σ V/p. The demagnetizing volume energy density is given by
| WD= –HDMS/2, | (1.2) |
| HD~= 4 π M, | (for thin film) |
where HD is the local demagnetizing field which appears inside the film due to the magnetic poles on the film surfaces (see Fig. 1.1), Ms is the saturation of magnetization and HD simple approximation by the mean value of magnetization vector M. For an infinite homogeneously magnetized film HD=-4 πMs and WD=2 π M2s. But, as it could be shown for thick enough film (d>>p), the demagnetizing field decays as Exp(-2z/p) with the distance (z) from the surface to the interior. So, the demagnetization energy of is non-zero in the layer of depth p/2 or in the volume Vdem=2LxLyp/2= LxLyp= LxLydp/d=Vp/d, here the coefficient 2 appears because of the two film surfaces (magnetic poles are located on the both film surfaces: on the top and bottom ones). Notice, the demagnetizing energy is always positive and namely this increases the total system energy. To decrease the magnetostatic energy a ferromagnetic sample is divided into domains. For example, for a thick film with a stripe domain structure the magnetostatic volume energy density is less than 2 π M2s and it can be written as Wm= η 2 π M2s , where η is a numerical coefficient. Rigorous calculations give η=0.136 (Kittel, 1946). The demagnetizing energy of the film with the stripe domains is Em= η 2 π M2sVdem= η 2 π M2sVp/d. Finally, collecting and inserting the obtained expressions for Ew and Ed into Eq. 1.1, one can arrive at
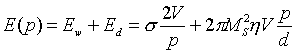 |
(1.2) |
Obviously, this energy has the minimum because it goes to infinity as p–>0 (too many domain walls) and as p->infty (infinite large Ed). The equilibrium domain size p0 is found by virtue of minimization of Eq. 1.2 with respect to p:
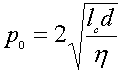 |
(1.3) |
where lc=σ/ 4 π M2s is the characteristic length which represents the key material parameter controling the domani size. In accord with Eq. 1.3 doman sizes are typically 10-4-10-6 cm. It follows from Eq.3 that for films of micrometer thickness the domain size grows as d1/2. Applying an external magnetic field (H) one can change the doman sizes because of an additional contribution – the energy of interaction between the magnetic moments and the applied field (Wz=-MH , Zeeman energy). This energy should be taking into consideration in Eq. 1.2.
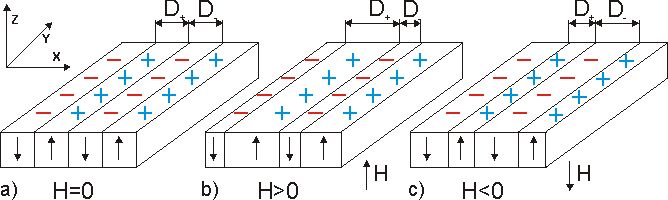
Fig. 1.2. Stripe domain structure of a film.
Domain structure in external magnetic field
The external magnetic field favors the domains in which the magnetization vector coincides with the field direction. In order to decrease the Zeeman energy these domains will increase their sizes while the domain magnetized in the opposite direction will be squeezed by the field. It is demonstrated in Fig. 1.2 (b and c). The film magnetization (the mean magnetic moment per unit volume) depends of the field and it is the simple relation between the volumes of “up” and “down” – magnetized domains with the size D+ and D–, respectively. So, it is
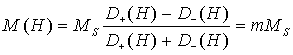 |
(1.4) |
where m is the normalized film magnetization. The magnetization process is the changes of the film magnetization M(H) with the changes of the applied field. Magnetization processes are characterized by the magnetic susceptibility.
By definition the magnetic susceptibility is χ=M/H (or more precisely χ=dM/dH). In order to calculate M(H) and χ let us consider a simplified case when the domain walls have negligible small energy. In this case the total energy as the sum of demagnetizing energy and energy of the external magnetic field H
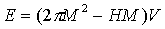 |
(1.5) |
By virtue of minimization of Eq. 1.5 with respect to M one can obtain the normalized film magnetization as
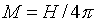 |
(1.6) |
Analysing the Eqs. 1.4,1.6 one can deduce : (i) when H=0 M=0 what is realised for D+=D–; (ii) by the definition χ=1/4π; (iii) increasing field volume of domain with magnetization along H increases and finally film is saturated (film undergoes into monodomain state) when H approaches 4 π MS The Animation shows the magnetization process in a garnet film. More precise domain description is presented in the level 3.