Interesting problem is describe magnetic material magnetization process, and define relationship magnetization M(H) depending on external magnetic fields H. For solving this problem we need knowledge about magnetic domain structure. We consider model based on sample with thickness h (Picture O1). The magnetization M measurred as a macro value we involve with domain structure size d+ i d–:
M=Ms*(d+ -d–)/(d+ +d–)=Ms*m ~~
where Ms is a magnetization of saturation which occur in single domain. On this page we can show changeability domain structure d+(H) id– (H) as esily as possible. On the next/linked pages we give precisly mathematic equations helpful for domain structure descriptions and software for aid this problem
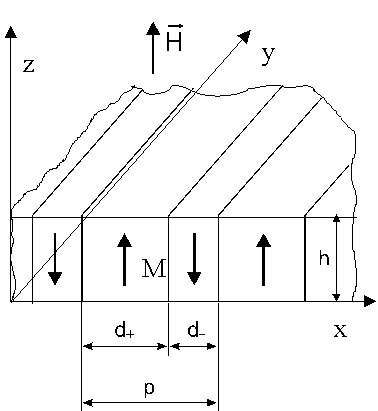
Rys. O1 Struktura domenowa w polu magnetycznym H
On the start we introduce concept energy of unit sample surface E. Applying magnetic fields with force lines perpendicular to sample surface we incrase volume of domain with the same direction of manetization vector. Respecting domain structure geometry introduced on picture O1 we can easy define energy of unit sample surface in magnetic fields H Eh=-h*H*m*Ms. (Or1)
With border between light and dark domains (domain wall) is associate energy [1]. For the unit sample surface we have energy Sw. Repeated analysis geometry from picture O1 give in simple way define the energy of the domain wall (unit of surface our layer) as:
Ew=2*h*Sw/p(Or2)
For the sake of domain wall good for minimum enrgy is incrase period of magnetic structure p.
More dificult to understend (mostly in mathematics structure) is take into consideration division magnetic material onto separately, light and dark doamins. It is a result magnetostatic influence its magnetic domain parts. Each one give magnetic fields (demagnetisation fields Hd) in whole space and in neighbouring areas of sample too. This field want arrange in these areas magnetisation in antiparallel direction to domain magnetisation. Demagnetization field try to make most as possible numbers of domain, and decrace period of structure p=d+ + d–. Simple mathematical description for demagnetization field and demagnetization energy Ed can introduce in case ‘ideal’ magnetic layer
Hdi=-4*Pi*M=-4*Pi*m*Ms (Or3a)
and demagnetization energy
Edi=2*Pi*h*m2*Ms2 (OR3b)
For derive formula Or3b we use the equation Or1 where field H changing by Hd and result two times decrase (interaction parts/areas of the sample). In the sample with homogenous magnetization |Hdj|=4*Pi*Ms and demagnetization energy have the biggest as possible valueEdj=2*Pi*h*Ms2. In the case domain structure with any period demagnetization energy we can describe by formula:
Ed= 4*Pi*h*Ms2 *F(h/p,m) (Or3c)
The exactly form of function F(h/p,m) is given on the next pages.
When we known magnetization of saturation Ms, domain wall energy Sw and thickness of magnetic layer h we can calculate two geometric parameters of structure: m(H) and p(H) (or d+(H) and d– (H)).To do this we look the minimum of complet layer energy Et which is a sum of energy Eh + Ew + Ed=Et. We introduce relationship beetween two “domains” parameters m and p from four quantities (three materialsMs, Sw, h and magnetic fields H) is on the first look very complicated problem If we take the Et form we can see that the problem can be simplify by reduced uantities. This way permit reduce problem to analyse geometric parameters of structure as a analyze function two parameters: material and reduced magnetic fields. When we divide Et by 4*Pi*h*Ms2 then:
Etn(l/h,hg,m,h/p)=Et/(4*Pi*h*Ms2) = 2*(l/h)*(h/p) Hg*m + F(m,h/p) (Or4e)
where parameter
- l=Sw/(4*Pi*Ms2) have a value of length and is known as a characteristic length and describe relation between domain wall energy and demagnetization energy in monodomain layer. l give also information about size of period p. Picture O4 showing relationshipp/h from l/h
- H*=H/(4*Pi*Ms) describe relation between H and demagnetization field Hd for monodomains sample.
The example of relationship magnetization curve m(H*) and the inverse domain structure period h/p(H*)is showing on the picture O2a i O2b. From this picture we see that with incrase l/h (domain wall energy) is more easy magnetize the layer, period in domain structure is bigger too. With incrase magnetic field decrase size of structure with magnetization in opposite directions, and increase the size of domain with magnetization consistent with H and structure period. From some value of magnetic fields period is infinite and sample have homogenous magnetization (pic O2, O3)
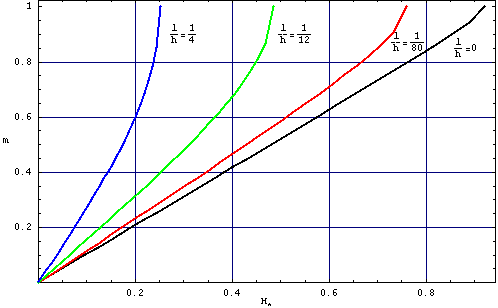
Rys. O2a. Relationship between reduced magnetiation m=(d+-d–)/(d++d–)) from field H*(=H/(4*Pi*Ms)) for different value l/h parameter.
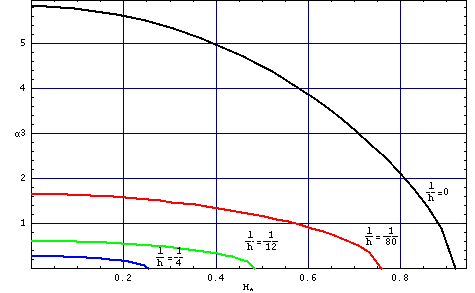
Rys. O2b. Relationship the normalized domain structure period inverse h/p from the H*(=H/(4*Pi*Ms)) for various values of l/h.
(a) 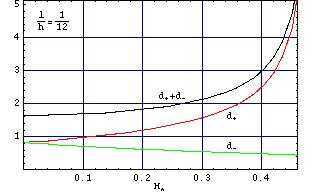 |
(b) 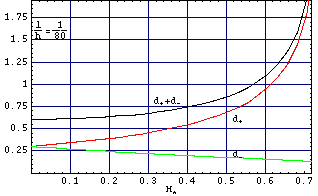 |
Rys. O3. Relationship the domain width d+ /h and d–/h from aplitude applied magnetic fields H*(=H/(4*Pi*Ms)). It is another presentation of results which we can see on the picture O2. Size of magnetic domain was calculated for value l/h=1/12 (a) and l/h=1/80.
Often in magnetization process describe is introduced idea of initial susceptibility chi0=M/H . It is ratio magnetization and magnetic fields which trigger this magnetization. In case ideal layer, is easy base on formula Or4 (ehre F(m)=0.5m2) calculate chi0i=1/4Pi. The same result we can obtain from picture 02a analyse. The picture 05 illustrate initial susceptibilityfrom h/p parametr.
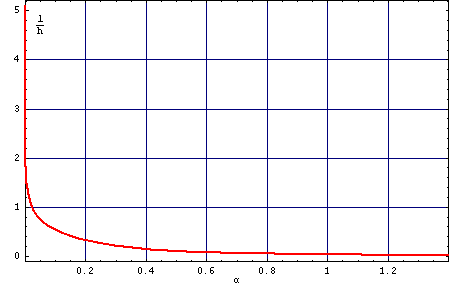
Pic O4. Relationship material parameters l/h from inverse of normalized domain structure period (in null magneic fields) h/p.
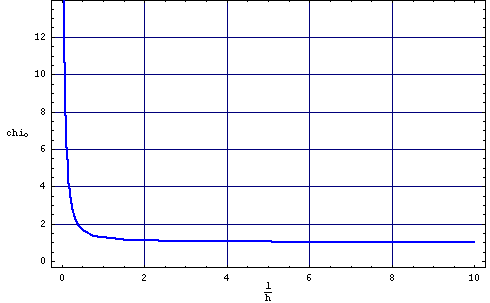
Pic. O5. Relationship initial susceptibility chi0 from material parameter l/h .
In the Internet experiment is possible, directly by picture of domain structure recording determine changebility in magnetic fields size d+and d– parameters in the “white” and “black” domains. It permit on determine domain structure period p and initial suscebility chi0, more precise chi0/Ms (because we calculate m(H)). Using this parameters in next step we can calculate materials parameters Ms and Sw. Calculate chi0 from analyse changebility domain structure is more easy using another option our experiment – measure the histeresis loop of the sample .
Formulas and software helpful in domain changebility analyse
Calculated values w and h which can see in generated graphs dane.zip (name indicates the value of the parameter l/h)
Additional bibliography:
- Encyklopedii Fizyki Współczesnej, PWN Warszawa, 1983, Artykuły:
“Struktura domenowa i procesy magnesowania”, H. i R. Szymczakowie, s 585
“Magnetooptyka”, W. Wardzyński, s 590