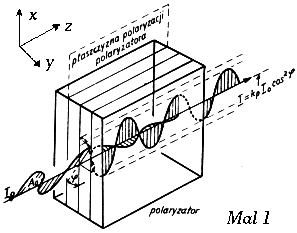
Wizualizacja domen magnetycznych w naszym zestawie pomiarowym wymaga stosowania układu polaryzator – analizator. Zestaw umożliwia również zmianę kąta alfa pomiędzy osią maksymalnego przepuszczania polaryzatora i analizatora. Taka konfiguracja, poza głównym celem jakim jest badanie domen, umożliwia więc także przeprowadzenie doświadczenia którego celem jest potwierdzenie prawa Malusa.
Na rysunku obok mamy schematycznie przedstawioną liniowo spolaryzowaną falę elektromagnetyczną przechodzącą przez polaryzator. Padająca fala zostaje częściowo wygaszona – przechodzi jedynie składowa amplitudy fal (wektora elektrycznego E) równoległa do płaszczyzny głownej polaryzatora (na rysunku m1 oś x). Zmianę natężenia światła można łatwo wyprowadzić rzutując wektor elektryczny E na oś przepuszczania i zakładając proporcjonalność I do kwadratu E.
I(delta)=I0 Cos2(delta)
gdzie I0 – natężenie światła padającego na polaryzator, delta – kąt pomiędzy płaszczyzną polaryzacji i osia przepuszczania polaryzatora
Tego typu związek został sformułowany już w 1810 roku przez Malusa i jest nazywany obecnie prawem Malusa.
W naszym eksperymencie możemy mierzyć natężenie I(alfa H) w funkcji kąta alfa (kąt pomiędzy płaszczyznami głownymi polaryzatora 1 i polaryzatora 2) i natężenia pola magnetycznego H przykładanego do próbki. Korzystając z prawa Malusa I można zapisać jako:
I(alfa)=I0 Cos2(alfa +fisr)
gdzie fisr – jest kątem skręcenia płaszczyzny polaryzacji światła przechodzącego przez próbkę. fisr zależy od magnetyzacji próbki m, którą możemy zmienić regulując wartość pola H; fisr = fi * m(H)
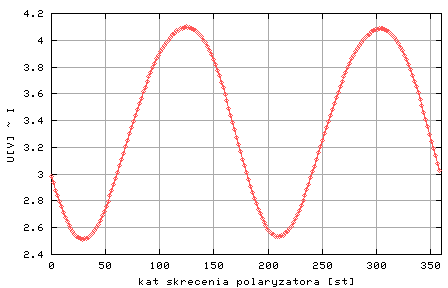
Rysunek Mal2:Przykładowy wynik pomiarów natężenia światła przechodzącego przez próbkę magnetyczną w funkcji kąta położenia polaryzatora alfa 1 =(alfa +alfa 0)
Wykonanie pomiaru
W celu wykonania pomiaru należy uruchomić program sterujący doświadczeniem: „Pomiar natężenia światła w funkcji położenia polaryzatora i natężenia pola magnetycznego”, a następnie wykonać pomiar przy dowolnie ustawionej wartości amplitudy pola magnetycznego (np 0 [A/m]). Wynikiem pomiaru są odpowiadające sobie dwa ciągi U(i) i alfa1(i) (1 <i <N, w naszym eksperymencie N=200). U(i) jest wartością napięcia mierzonego przez detektor światła (wartością podawaną w woltach) i wiąże się z natężeniem światła I liniową relacją:
U = a+b*I
alfa1(i) określa położenie polaryzatora, w którym dokonano pomiaru U(i).
Po zakończonym pomiarze komputer standardowo wykreśla zależność U(alfa1), Przykładowa prezentacja wyników widoczna jest na rysunku Mal 2. Na stronie Pomiar natężenia światła w funkcji położenia polaryzatora i natężenia pola magnetycznego istnieją jeszcze dwie dodatkowe opcje zapoznania się z uzyskanymi wynikami :
- obejrzenie tabelki zawierającej trzy kolumny: i, U(i), alfa1(i);
- import danych do komputera Internauty
Sprawdzenia prawa Malusa mozemy dokonać porównując zmierzone wartości U(alfa1(i)) z wartościami teoretycznymi UT(alfa1(i)) wyliczonymi ze wzoru:
UT(alfa1) =a +b0 * Cos2(alfa1+alfa0)
Problem sprowadza się do znalezienia trzech parametrów U1, U0 i alfa0 by zależność teoretyczna UT(alfa1) jak najlepiej opisywała wyniki przeprowadzonego doswiadczenia. Do oszacowania tych parametrów można zwrócić uwagę na maksymalne i minimalne wartości U:
- średnia wartość U określa a
- róznica U maksymalnej i minimalnej wyznacza b0
- przesunięcie minimum na osi alfa 1 pozwala na określenie alfa0
W celu precyzyjnego określenia (dopasowania – „dofitowania” od angielskiego słowa „fitting”) parametrów U1, U0 i alfa0 poszukuje się minimum sumy (U(alfa(i)) -UT(alfa(i)))2. Istnieją specjalne metody numeryczne pozwalające na znalezienie tego minimum. Dalej proponowane jest wykorzystanie w tym celu bezpłatnie dostępnego programu GnuPlot Na rysunku Mal 3 widać, że dopasowana krzywa teoretyczna nieźle opisuje wyniki doświadczalne.
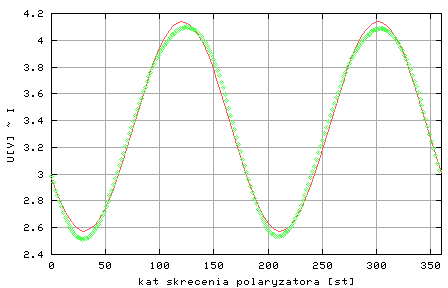
Rysunek Mal 3 : Uzyskana z prawa Malusa krzywa teoretyczna (linia ciagła) dopasowana do wyników eksperymentalnych.
Przykładowy program w języku programu Gnuplot do dopasowania naszych wyników:
set angles degrees
fun(alfa1) = a + b0*cos(alfa1+alfa0 )**2
fit fun(alfa1) „dane.dat” via „par.dat”
Polecenie set angles degrees określa sposób zapisywania kątów ( w stopniach nie w radianach które są domyślne dla większości programów komputerowych). Postać funkcji uwzględnia takie parametry jak: przesunięcie poziomu sygnału – U1, skalowanie funkcji cos – U0 i przesunięcie fazy – parametr alfa1. Kolejna linia wywołuje dopasowanie „fit” które do danych zawartych w pliku dane.dat dopasowuje funkcję fun(alfa1). Plik par.dat spis początkowych wartości parametrów użytych wfunkcji fun(x).
a = 2.6
b0 = 1.4
alfa0 =-60
Program gnuplot można ściągnąć spod tego adresu: http://www.gnuplot.info