Cyfrowa analiza obrazów domen magnetycznych – poprawa kontrastu obrazu struktury domenowej
Obraz cyfrowy U jest dwuwymiarową macierzą o wymiarze W x S (w naszym eksperymencie 368×286) gdzie każdy jej element U(i,j) jest nazywany pikselem. W czasie procesu wyświetlania obrazu na ekranie tworzona jest graficzna reprezentacja tej macierzy gdzie każdy piksel ma wartość powiązaną z odcieniem szarości (obraz monochromatyczny) lub kolorem. Zazwyczaj używa się kodowania ośmio bitowego dla obrazu w skali szarości i dwudziestocztero bitowego dla obrazu skali RGB ( 8 bitów na każdy kolor R- red – czerwony, G – green – zielony, B -blue – niebieski).
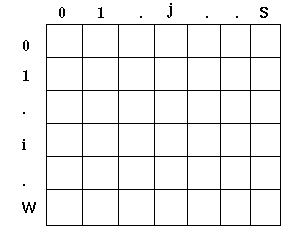
Siatka reprezentujaca sposób rozmieszczenia danych w macierzy o wymiarze SxW i przykładowy piksel U(i,j) obrazu. Lewy górny róg obrazka odpowiada zazwyczaj punktowi o współrzędnych (0,0).
Do zamiany obrazu na postać cyfrową można posłużyć się różnego rodzaju urządzeniami. Najbardziej rozpowszechnione sa skanery, choć ostatnio, także ze względu na coraz mniejsze koszty używane sa do tego różnego rodzaju „grabery” obrazu video pochodzącego z kamer, odbiorników TV czy magnetowidów. Pozwala to dzięki odpowiednim przetwornikom analogowo – cyfrowym wbudowanym w te urządzenia zamieniać sygnał video na postać cyfrową czyli na sekwencje klatek – macierzy reprezentujących obraz w tej postaci. Poza ilością bitów potrzebnych do zakodowania koloru w opisie cyfrowego obrazu istotny jest także jego rozmiar podawany jest w liczbie piksli jaka przypada na szerokość i wysokość obrazu (podawany często parametr SZEROKOŚĆ x WYSOKOŚĆ). Ilość piksli w obrazie cyfrowym oddaje też informację o jakości (dokładności) z jaką realny obraz przenoszony jest do komputera.
a) |
b) |
Reprezentacja graficzna obrazów. Na rysunku (a) widzimy powiększony fragment struktury domenowej na którym możemy zauważyć poszczególne piksle. Obraz został przedstawiony w ośmio poziomowej skali szarości. Na rysunku (b) pokazana jest macierz danych powiększonego fragmentu. Liczby odpowiadają odpowiednim poziomom szarości.
W naszych rozważaniach skupimy się na obrazach w których kolor będzie reprezentowany w postaci skali szarości kodowanej ośmioma bitami (256 odcieni szarości). Przejścia do skali szarości z obrazu cyfrowego zapisanego w skali RGB można dokonać na trzy różne sposoby obliczając dla każdego piksla:
- luminacjęY:
Y = 0.3R + 0.59G + 0.11B
- desaturację L
L = (Max(R, G, B) + Min(R, G, B))/2
- dekompozycję V
V = Max(R, G, B)
W przypadku gdy rejestrowany obraz jest zaszumiony (np zakłócenia sygnału video, słabe oświetlenie) istnieje możliwość poprawy jego jakości. Można to osiągnąć przez sumowanie odpowiedniej liczby klatek w celu wyciągnięcia wartości średniej w każdym punkcie (pikslu). Jest to oczywiście możliwe wtedy gdy rejestrowany przedmiot jest nieruchomy, a tak właśnie jest w przypadku domen magnetycznych.
Histogram h(k) jest funkcją którą możemy posłużyć sie w celu oceny liczebności piksli danego koloru k w całym obrazie. W najprostszej definicji h(k) = N gdzie N jest liczba danego koloru a k ={0..kmax} (kmax -liczba kolorów). W przypadku obrazów w skali szarości mamy więc kmax=256 czyli 256 kanałów do których mozemy przypisać liczbę wystąpień danego koloru. W przypadku obrazu domen magnetycznych gdzie część z nich jest ciemna, a druga jasna funkcja ta daje nam możliwość oceny poziomu separacji miedzy nimi, co ułatwia także wyboru poziom progowania.
 |
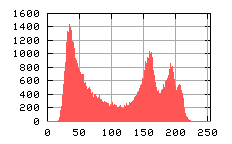 |
Obraz domeny w skali szarości i jego histogram – przykład dotyczy obrazu z N=30 krotnym sumowaniem
W przypadku gdy jedynie część obszaru obrazu niesie informację na temat nas interesujący można dokonać wycięcia – maskowania pozostałej jego części (poniższy rysunek). W celu poprawienia jakości – pozbycia się szumów można też dokonać wielokrotnego zsumowania rejestrowanych obrazów. Obraz wynikowy Uś zapisuje się jako:
Uś(i,j) = 1/N*Suma( Uk(i,j),{k,1,N})
Gdzie Ui są kolejnymi sumowanymi obrazami. Oczywiście możliwe jest to gdy obserwowany obiekt nie ulega zmianom (przynajmniej w czasie rejestracji). Wynik takiej operacji widoczny jest także w histogramie obrazu w postaci lepiej zlokalizowanych „pików” odpowiadających każdej z domen.
a)  |
 |
b)  |
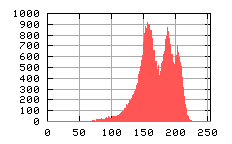 |
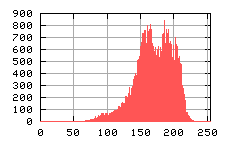
Obrazy domen i ich histogram – przykład poprawienia jakości obrazu w wyniku sumowania (obrazy z maskowanym – wyciętym obszarem poza domenami. W przypadku (a) brak sumowania, (b) sumowanie 20-to krotne. Na histogramach widać poprawę jakości obrazu (dokładniej zdefiniowane odcienie szarości występujące w obrazie)
Metodą na podniesienie kontrastu a także na wyeliminowanie niejednorodności związanych z oświetleniem próbki jest różnicowanie dwóch obrazów Umax i U. Pierwszy z nich to obraz próbki w przypadku gdy jest wytworzona monodomena – próbka przenagnesowana całkowicie w jednym kierunku, drugi to obraz domeny w dowolnym polu magnetycznym. Ich wynik UR jest odjęciem piksel po pikslu według zależności:
UR(i,j) = Umax(i,j) -U(i,j)
Umożliwia to „wyciągnięcie” informacji tylko na temat różnicy poziomów szarości związanych z gęstościa optyczną wytworzonych domen.
a)  |
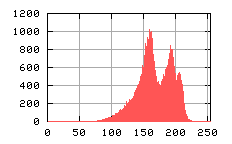 |
b) 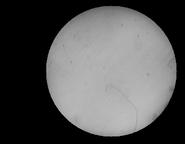 |
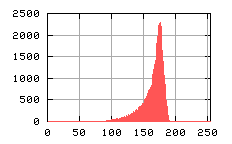 |
c)  |
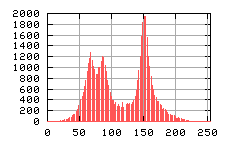 |
Inna metodą, która jest charakterystyczna dla obróbki obrazów domen magnetycznych jest zastosowanie tzw.metody dwupołożeniowej. Polega ona na zarejestrowaniu dwóch obrazów U1 i U2 domen magnetycznych obserwowanych pod katem +fi i -fi w stosunku do położenia skrzyżowania płaszczyzn polaryzatora i analizatora i poddaniu ich operacji:
UD(i,j) = ( U1(i,j) – U2(i,j))/( U1(i,j) +U2(i,j))
której końciowym wynikiem jest obraz UR. Metoda ta pozwala na podniesienie kontrastu między obszarami przeciwnie namagnesowanych obszarów.
a)  |
 |
b)  |
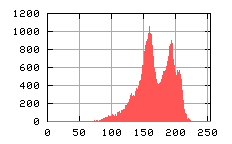 |
c)  |
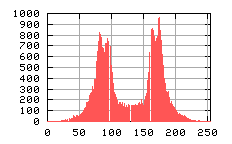 |
Metoda dwupołożeniowa. na rysunkach a) i b) obrazu domen U1 i U2 zarejestrowane dla katów +fi i -fi. Na rysunku c) przedstawiony jest wynik końcowy. Na histogramie obok widać zmianę w rozkładzie odcieni szarości na wynikowym obrazie.
Zarówno metoda różnicowania obrazów jak i metoda dwupołożeniowa wymagaja przeniesienia wyniku operacji arytmetmetycznych z uzyskanego przedziału (Min(U(i,j)),Max(U(i,j))) na zakres 0 ÷ 255 (poziomy szarości w plikach typu greyscale). Dokonuje się tego poddając go operacji:
Uk(i,j) = (U(i,j)+Min(U(i,j)))/(Min(U(i,j))+Max(U(i,j))) *255
gdzie Uk jest obrazem końcowym, Min(U(i,j)) – element minimalny U, Max(U(i,j)) – element maksymalny U