Interesującym zadaniem jest opisanie procesu magnesowania magnetyka, określenie zależności namagnesowania M(H) w zależności od amplitudy przyłożonego pola magnetycznego H. Do rozwiązania tego zadania konieczna jest znajomość struktury domenowej magnetyka. Rozważmy model struktury domenowej próbki o grubości h z rysunku O1. Makroskopowo mierzoną magnetyzację próbki M wiążemy z rozmiarami struktury domenowej d+ i d–:
M=Ms*(d+ -d–)/(d+ +d–)=Ms*m ~~
gdzie Ms jest magnetyzacją nasycenia jaka występuje w pojedynczej domenie. Na tej stronie przedstawio, odwołując się bardziej do intuicji Internauty, zmienność struktury domenowej d+(H) i d– (H). Wprowadzone jest pojęcie energii E jednostki powierzchni próbki. Na dołączonych stronach podano też precyzyjny aparat matematyczny pomocny do opisu struktury domenowej oraz wspomagające programy komputerowe.
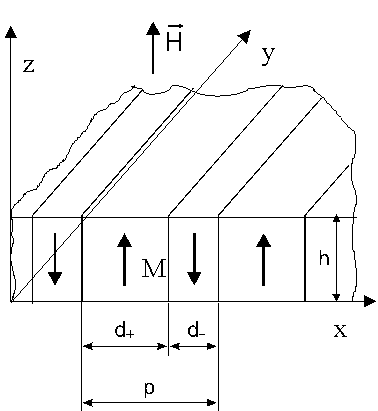
Rys. O1 Struktura domenowa w polu magnetycznym H
Przykładając pole magnetyczne zwiększa się objętość domen o magnetyzacji zorientowanej wzdłuż pola. Uwzględniając geometrię naszej struktury domenowej z Rys.O1 łatwo można opisać energię jednostki powierzchni próbki w polu H wzorem:
Eh=-h*H*m*Ms. (Or1)
Z granicą pomiędzy domenami ścianą domenową związana jest pewna energia [1]. Jednostce powierzchni ściany odpowiada energia Sw. Ponowna analiza geometrii struktury domenowej rys.O1 pozwala w prosty sposób określić energię ściany domenowej (jednostki powierzchni naszej warstwy) jako
Ew=2*h*Sw/p(Or2)
Ze względu na ścianę domenową energetycznie jest korzystne zwiększenie periodu p struktury domenowej.
Trudniejsze w zrozumieniu a zwłaszcza w opisie matematycznym jest uwzględnienie podziału magnetyka na domeny. Jest to wynik magnetostatycznego oddziaływania jego poszczególnych części domen magnetycznych. Każda domena wytwarza pole magnetyczne (pole odmagnesowania Hd) w całej przestrzeni w tym również w sąsiednich obszarach próbki. Pole to stara się ustawić w tych obszarach magnetyzację antyrównolegle do magnetyzacji w domenie. Pole odmagnesowania dąży więc do utworzenia jak największej ilości domen, do zmniejszenia periodu struktury p=d+ + d–. Prosty matematycznie opis pola odmagnesowania i energii odmagnesowania Ed można przeprowadzić w przypadku warstwy „idealnej”
Hdi=-4*Pi*M=-4*Pi*m*Ms (Or3a)
a energia odmagnesowania
Edi=2*Pi*h*m2*Ms2 (OR3b)
Do wyprowadzenia wzoru Or3b skorzystano ze wzoru Or1 gdzie pole H zamieniono przez Hd i wynik dwukrotnie zmniejszono (efekt wzajemnego oddziaływania poszczególnych obszarów próbki). W próbce jednorodnie namagnesowanej |Hdj|=4*Pi*Ms a energia odmagnesowania przyjmuje największą z możliwych wartości Edj=2*Pi*h*Ms2. W przypadku struktury domenowej z dowolnym periodem energię odmagnesowania można opisać wzorem :
Ed= 4*Pi*h*Ms2 *F(h/p,m) (Or3c)
Konkretna postać funkcji F(h/p,m) podana jest na kolejnych stronach.
Znając magnetyzację nasycenia Ms, energię ściany domenowej Sw i grubość warstwy h można wyliczyć dwa parametry geometryczne struktury m(H) i p(H) (lub d+(H) i d– (H)). W tym celu zwykle poszukuje się minimum całkowitej energii warstwy Et będącej sumą energii Eh + Ew + Ed=Et. Prezentacja zależności dwóch parametrów „domenowych” m i p od czterech wielkości (trzech materiałowych Ms, Sw, h oraz amplitudy pola H) wydaje się w pierwszym momencie zadaniem dosyć skomplikowanym. Z postaci energii Et widać jednak, że zadanie to można znacznie uprościć wprowadzając zredukowane wielkości. Pozwala to na sprowadzenie analizy parametrów geometrycznych struktury do analizy funkcji dwóch parametrów jednego materiałowego i zredukowanego pola magnetycznego. Podzielmy Et przez 4*Pi*h*Ms2 wówczas:
Etn(l/h,hg,m,h/p)=Et/(4*Pi*h*Ms2) = 2*(l/h)*(h/p) Hg*m + F(m,h/p) (Or4e)
gdzie parametr
- l=Sw/(4*Pi*Ms2) o wymiarze długości jest tak zwaną długością charakterystyczna określa stosunek energii ściany domenowej do energii odmagnesowania monodomenowej warstwy; l niesie informację o wielkości periodu p, rysunek O4 pokazuje związek p/h od l/h
- H*=H/(4*Pi*Ms) opisuje stosunek pola H do pola odmagnesowania Hd monodomenowej próbki.
Przykładowe zależności krzywej magnesowania m(H*) i odwrotności periodu struktury domenowej h/p(H*) przedstawiają rysunki O2a i O2b. Z rysunków tych widać, że ze wzrostem parametru l/h (wzrostem energii ściany domenowej) łatwiej jest magnesować warstwę, większy jest period struktury domenowej. Period struktury domenowej jest najmniejszy w zerowym polu magnetycznym. Ze wzrostem pola maleje rozmiar struktury z magnetyzacją przeciwnie skierowaną do pola, rośnie rozmiar domen z magnetyzacją zgodną z H oraz period struktury. Od pewnej wartości pola period jest nieskończony próbka staje się jednorodnie namagnesowana, rys. O2, O3
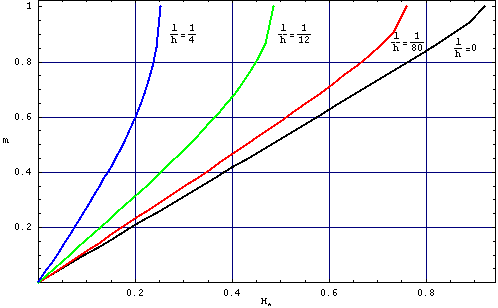
Rys. O2a. Zależność zredukowanej magnetyzacji m=(d+-d–)/(d++d–)) od pola H*(=H/(4*Pi*Ms)) dla różnych wartości l/h.
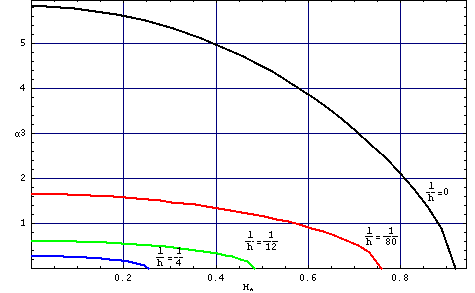
Rys. O2b. Zależność odwrotności znormalizowanego periodu struktury domenowej h/p od pola H*(=H/(4*Pi*Ms)) dla różnych wartości l/h.
(a) 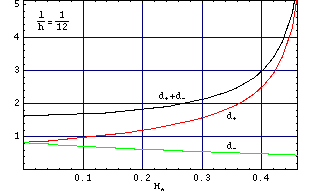 |
(b) 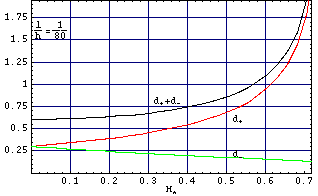 |
Rys. O3. Zależność szerokości domeny d+ /h i d–/h od amplitudy przyłożonego pola magnetycznego H*(=H/(4*Pi*Ms)). Jest to inna prezentacja wyników podanych na rysunku O2. Rozmiary domen wyliczono dla wartości l/h=1/12 (a) i l/h=1/80.
Często do opisu procesu magnesowania, jego łatwości, wprowadza się pojęcie podatności początkowej chi0=M/H jest to stosunek magnetyzacji do pola H, które tą magnetyzację wywołało. W przypadku warstwy idealnej łatwo jest, na podstawie wzorów Or4 (gdzie F(m)=0.5m2), wyliczyć chi0i=1/4Pi, wynik ten można też uzyskać z analizy rysunku O2a. Rysunek O5 ilustruje zależność początkowej podatności od h/p.
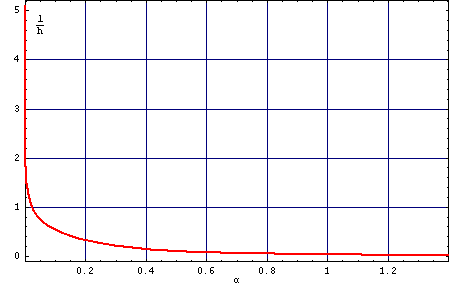
Rys. O4. Zależność parametru materiałowego l/h od odwrotności znormalizowanego periodu struktury domenowej (w zerowym polu magnetycznym) h/p.
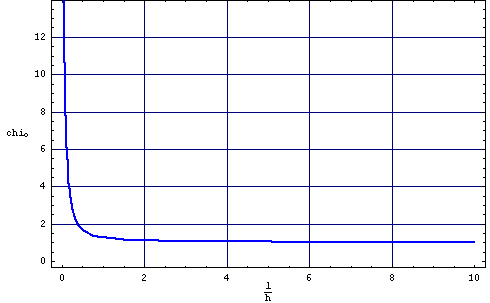
Rys. O5. Zależność podatności początkowej chi0 od parametru materiałowego l/h .
W Internetowym doświadczeniu można, poprzez bezpośrednią rejestrację obrazów struktury domenowej , wyznaczyć zmienność w polu magnetycznym rozmiarów d+ i d– domen „białych” i „czarnych”. Pozwala to na wyznaczenie periodu struktury p i początkowej podatności chi0, precyzyjniej chi0/Ms (gdyż wyliczamy m(H)). Korzystając z powyższych rozważań można w kolejnym kroku wyliczyć parametry materiałowe badanej warstwy Ms i Sw. Wyliczanie chi0 z analizy zmienności struktury domenowej jest procedurą dosyć żmudną. Znacznie prościej można to uczynić korzystając z innej opcji naszego internetowego eksperymentu pomiaru krzywej magnesowania.
Wzory i programy pomocne w analizie zmienności domen
Wyliczone wartości w i h użyte do generacji wykresów: dane.zip (nazwa wskazuje na wartść parametru l/h)
Polecana dodatkowa literatura :
- Encyklopedii Fizyki Współczesnej, PWN Warszawa, 1983, Artykuły:
„Struktura domenowa i procesy magnesowania”, H. i R. Szymczakowie, s 585
„Magnetooptyka”, W. Wardzyński, s 590