Now technologies allow us to create artificial materials and nanostructures which are absent in the Nature. Such nanostructures could be built on the atomic level by a precise deposition of small group atoms (atomic layers) and even isolated atoms on a specially prepared substrate. During the deposition one can combine atoms of different chemical elements, for example, to produce sandwiches from magnetic and non-magnetic atomic layers or sandwiches of a few magnetic atomic layers covered by layers of non-magnetic metals (see Fig.2.1).
 |
| Fig. 2.1. Quasi-2D nano-sandwich constructed from the atomic layers of different chemical elements (the different elements marked in different colors). |
Magnetic properties of such nanoobjects are quite unusual and puzzled. Moreover, such magnetic nanostructure, e.g. ultrathin magnetic films have a huge application potential, e.g. in magnetic memory storage and recording devices.
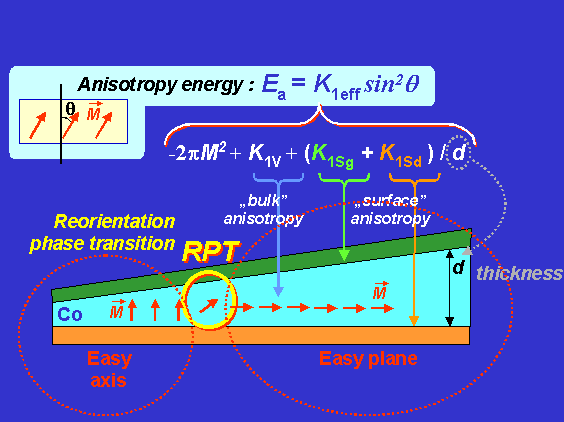 |
| Fig. 2.2. Magnetic cobalt nanowedge (schematically). The arrows show the orientation of magnetization vector. On the left (thinner part), the magnetization state is perpendicular one, while on the right (thicker part), in-plane. The contributions from the “top” and “bottom” surfaces to magnetic anisotropy are shown. |
Magnetic perpendicular anisotropy of ultrathin ferromagnetic films is one of fundamental interests of magnetism of low dimensional systems (with dimensions between 2D and 3D). Magnetization states, depending on film thickness, are illustrated in Fig.2.2. For ultrathin film the anisotropy energy EA is described in the following form 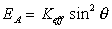 .
.
There are different sources for the anisotropy rising: crystalline (or “bulk” anisotropy), the surface anisotropy due to the broken symmetry; shape anisotropy and etc. These contributions in different ways depend on the film thickness. It is commonly assumed to describe the thickness dependence of the effective anisotropy energy of ultrahin films as
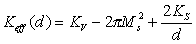 |
(2.1) |
where KV is the bulk “volume” anisotropy constant, Ks is the surface anisotropy constant. The second term in Eq.2.1 describes the demagnetization energy which is -2 Pi MS2, for film in the monodomain state. It is possible to realize vanishing of the constant Keff (/e.g. changing the film thickness)
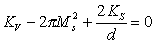 |
(2.2) |
So, at d=d1 (as Keff (d1 )=0). For cobalt films, depending on the grown condition, substrates and coverage, d1 typically varies from 1.5 to 1.8 nm.
Domain structures and magnetization processes for Co in an out-off plane state (d < d1 ) differ from those which observed in micron-sized films. Such films may exhibit a square type of hysteresis loop shown in Fig. 3.2. Domain structures could be formally described using the models from the previous chapter, see Eqs.1.14 and Eq.A2 and Eq.A3. It gives the domain period in the range from ~100 km to hundreds of nanometers as the cobalt thickness increases from d=0.8 nm to d1 ~= 1.79 nm [1]. However, for thinner films the domain structure geometry is mainly governed by coercivity rather than magnetostatic forces. Fig. 2.3 shows the domain structure registered without magnetic field in the cobalt film with d=0.8 nm [2] (d < d1)). One can see the domain size is much smaller than that predicted by the above theories. Such magnetic domain states are out-of-equilibrium but they are long-time living what could be very useful for applications. It is necessary to use quite different physical basis to describe domain geometry and magnetization processes – taking into account a spatial coercivity distribution one can numerically simulate domain structures in ultrahin films. The result of such simulations is shown in Fig.2.4 [2].
For d>d1 the magnetization vector lies into the film plane and the film becomes in-plane magnetized. There are no magnetic domains caused by magnetostatics. It is easy to describe magnetization process for d>d1. Let us consider a simplified case allowing the magnetization vector to coherently rotate in a homogeneously magnetized film. In this case the total film energy is given by
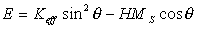 |
(2.3) |
where θ is the angle between the normal to the film surface and the magnetization vector, H is the magnetic field applied along the film normal. In equilibrium the inclination of magnetization from the film normal corresponds to the minimum of the energy (Eq.2.3). So,
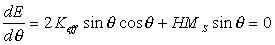 |
(2.4) |
By solution of Eq.2.4 we find the equilibrium magnetization orientation, θe as
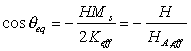 |
(2.5) |
where the normalized magnetization component perpendicular to the film plane linearly depend on magnetic field normalized by the anisotropy field, HA,eff = 2 Keff / Ms .
 |
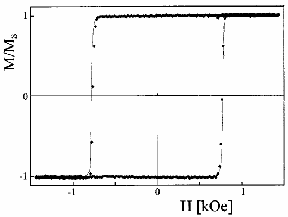 |
| Fig. 2.3. Domain structure of ultrathin cobalt with d=0.8 nm and the magnetic hysteresis loop obtained with using the Kerr effect [2]. | |
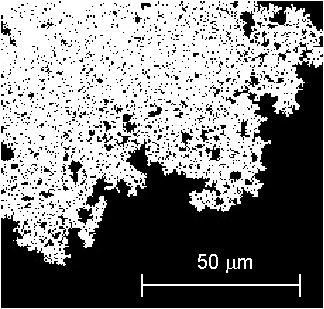 |
| Fig. 2.4. Simulated domain structure of ultrathin cobalt with d=0.8 nm [2]. |
References
- M. Kisielewski, A. Maziewski, T. Polyakova, and V. Zablotskii. Wide-scale evolution of magnetization distribution in ultrathin films. /Phys. Rev. B/ 69, 184419 (2004).
- J. Ferr�, V. Grolier, P. Meyer, S. Lemerle, A. Maziewski, E. Stefanowicz, S. V. Tarasenko, V. V. Tarasenko, M. Kisielewski and D. Renard. Magnetization reversal processes in an ultrathin Co/Au film /Phys. Rev. B,* */55, 22, 15 092 (1997).