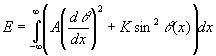
Magnetic anisotropy. Magnetocrystalline anisotropy is an intrinsic property of a ferromagnet, independent of and its shape. In can be most easily seen by measuring magnetization curves along different crystal directions. Depending on the crystallographic orientation of the sample in the magnetic field, the magnetization reaches saturation in different fields. The easy axis is the direction in which the sample could be easily magnetized, i.e. magnetized by the smallest applied field. In a simplest case the anisotropy energy could be described by only one angle defining the magnetization orientation with respect to the easy axis: Ea=K1 sin2θ+ K2 sin4θ, where K1 and K2 are the first and second anisotropy constants, respectively, and θ is the angle between the magnetization vector and easy axis.
The exchange energy. The exchange energy represents the adjacent spin-spin interaction that gives rise to ferromagnetism. Defined in terms of the gradient of the magnetization components, it is especially sensitive to the angle between two neighboring spins, φ. It is usually assumed that the parallel orientation of spins corresponds to zero of the exchange energy. The exchange energy does not depend on orientation of spins (magnetic moments) in the crystal. The volume density of the exchange energy is described by Eex=A(dφ/dx)2, where A is the exchange constant and x is a coordinate.
Domain wall energy. In a domain wall the magnetization vector, M gradually turns from its direction into one domain to the direction of M in the neighboring domain. Let us consider the one-dimensional case when the magnetization orientation depends on one coordinate. There are two main contributions to the energetic of the domain wall. The first, due to inclination of the magnetization from the easy axis and it is described by energy volume density Ea(x)=Ksin2θ(x). The second, rises because of the gradient of the magnetization component, Eex(x)=A(dφ/dx)2. The domain wall surface energy density is given by the integral over the wall space
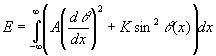 |
(1) |
The integral should be taken over an infinite distance and minimized under of the superimposed the boundary conditions θ(- ∞)=0 and θ( ∞)=π , those correspond to the antiparallel orientation of M in the two neighboring domains. Note, one should find a function θ(x) minimizing the integral (1). Such a procedure is called as minimization of a functional. The minimization of the functional (Eq.1) gives the domain wall energy as σ=4(AK)1/2. This is the surface density of the Bloch wall.
Zeeman energy is the
energy of a magnetic body in an external field, H. This energy is
given by 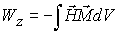 .
.
Demagnetizing (or magnetostatic)
energy. The magnetostatic energy is defined as 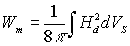 (the integral should
be taken over all space). In a multidomain state the magnetostatic energy is
less than that in the single domain state because of a large decrease in the
intergation volume (Vs ) occupied by the stray field.
(the integral should
be taken over all space). In a multidomain state the magnetostatic energy is
less than that in the single domain state because of a large decrease in the
intergation volume (Vs ) occupied by the stray field.
Stray field. Stray field is the magnetic field generated by the magnetic body itself. The sinks and sources of the magnetization work like positive and negative "magnetic" charges. There is analogy with an elecotrostatic field from electric charges. The stray field energy (or magnetostatic energy ) can be avoided by flux-closure domains (Landau and Lifshitz domain structure ).
Magnetic poles. The magnetic force surrounding a magnet is not uniform. There exists a great concentration of force at each end of the magnet and a very weak force at the center. Proof of this fact can be obtained by dipping a magnet into iron filings. It is found that many filings will cling to the ends of the magnet while very few adhere to the center. The two ends, which are the regions of concentrated lines of force, are called the poles of the magnet. Magnets have two magnetic poles and both poles have equal magnetic strength.
Ferromagnetic materials have a large and positive magnetic susceptibility to an external magnetic field. They exhibit a strong attraction to magnetic fields and are able to retain their magnetic properties after the external field has been removed. Ferromagnetic materials have some unpaired electrons so their atoms have a net magnetic moment.
Magnetic lines. Magnetic lines of force are lines which help visually represent a magnetic field. By convention, magnetic lines of force point from north to south outside a magnet (and from south to north inside a magnet). Magnetic lines of force form complete loops. They never cross.
'; ?>